 por anamendes » Dom Mai 06, 2012 09:10
por anamendes » Dom Mai 06, 2012 09:10
Tenho dificuldades em "visualizar" os intervalos nos quadrantes do círculo trigonométrico
Por exemplo:
]-pi;pi[
]-pi/2;pi/2[ Como faço para ver se é no 1º,2º,3º ou 4º quadrante?
]0;-3pi/2[
]-pi/2;pi[
-
anamendes
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sáb Abr 28, 2012 08:01
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ciências e tecnologias
- Andamento: cursando
 por Molina » Ter Mai 08, 2012 00:28
por Molina » Ter Mai 08, 2012 00:28
Boa noite, Ana.
Você pode transformar de radiano para graus, utilizando
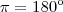
. Talvez assim você visualize melhor.
Seja o ciclo trigonométrico:

Do 0º ao 90º: 1º quadrante
Do 90º ao 180º: 2º quadrante
Do 180º ao 270º: 3º quadrante
Do 270º ao 360º: 4º quadrante
Começaremos SEMPRE do 0º. Quando o valor for positivo, o sentido que utilizaremos será anti-horário. Quando o valor for negativo, o sentido que utilizaremos será o horário.
Conseguiu visualizar?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



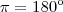 . Talvez assim você visualize melhor.
. Talvez assim você visualize melhor.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.