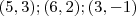 .
.

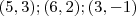 .
.
Claudin escreveu:Determine a equação da circunferência que contém os pontos.
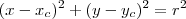
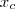 ,
, 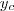 e r. E note também que o enunciado forneceu três pontos. Desse modo, substituindo os pontos você pode determinar um sistema:
e r. E note também que o enunciado forneceu três pontos. Desse modo, substituindo os pontos você pode determinar um sistema: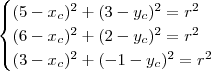


Claudin escreveu:Continuo não entendendo, porque no caso acima o ponto (6,2) não entra no sistema?



Claudin escreveu:Para resolver o sistema basta substituir o terceiro ponto no sistema? Não compreendi.
Claudin escreveu:Basta resolver o sistema
mas o problema agora é resolver o sistema
desde ontem que estou tentando e nada, expandi os produtos notáveis mas piorou a situação.

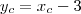
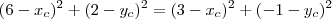
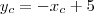
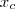 e
e 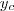 :
: 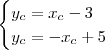

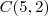
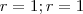
![r=\sqrt[]{13} r=\sqrt[]{13}](/latexrender/pictures/a4625ec5e13e12af21114d58b19fbd79.png)

Claudin escreveu:Encontre o Centro da circunferência sendo:
Substituindo no sistema de 3 equações acima obtive valores discrepantes:



Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes