Estou tentando calcular determinante de sistemas lineares.
Não sei se eu conto os números que estão do lado direito da igualdade, pois se eu montar uma matriz contando com eles, ela não fica quadrada.
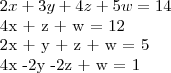
Sei que a determinante é -72.
Se eu calculo montando a matriz sem as igualdades (14,12,5,1), obtenho -124.
Alguém pode me ajudar?
Obrigado!!


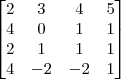


 .
.
 :
: