Peço ajuda no cálculo da derivada, pela definição, da função
![\sqrt[4]{x} \sqrt[4]{x}](/latexrender/pictures/c0e46d4c908766f6783b14291952c9c5.png) .
.Comecei por
![\lim_{h\rightarrow0}\frac{\sqrt[4]{x+h}-\sqrt[4]{x}}{h} \lim_{h\rightarrow0}\frac{\sqrt[4]{x+h}-\sqrt[4]{x}}{h}](/latexrender/pictures/6dcfefa247ee0971143234d435710008.png) . Depois tentei ir desenvolver, aplicando o conjugado do numerador, mas a partir daí não consegui avançar.
. Depois tentei ir desenvolver, aplicando o conjugado do numerador, mas a partir daí não consegui avançar.Obrigado!

![\sqrt[4]{x} \sqrt[4]{x}](/latexrender/pictures/c0e46d4c908766f6783b14291952c9c5.png) .
.![\lim_{h\rightarrow0}\frac{\sqrt[4]{x+h}-\sqrt[4]{x}}{h} \lim_{h\rightarrow0}\frac{\sqrt[4]{x+h}-\sqrt[4]{x}}{h}](/latexrender/pictures/6dcfefa247ee0971143234d435710008.png) . Depois tentei ir desenvolver, aplicando o conjugado do numerador, mas a partir daí não consegui avançar.
. Depois tentei ir desenvolver, aplicando o conjugado do numerador, mas a partir daí não consegui avançar.
emsbp escreveu:Peço ajuda no cálculo da derivada, pela definição, da função.
Comecei por. Depois tentei ir desenvolver, aplicando o conjugado do numerador, mas a partir daí não consegui avançar.
![\left[\left(\sqrt[4]{x+h}\right)^3 + \left(\sqrt[4]{x+h}\right)^2\left(\sqrt[4]{x}\right) + \left(\sqrt[4]{x+h}\right)\left(\sqrt[4]{x}\right)^2 + \left(\sqrt[4]{x}\right)^3\right] \left[\left(\sqrt[4]{x+h}\right)^3 + \left(\sqrt[4]{x+h}\right)^2\left(\sqrt[4]{x}\right) + \left(\sqrt[4]{x+h}\right)\left(\sqrt[4]{x}\right)^2 + \left(\sqrt[4]{x}\right)^3\right]](/latexrender/pictures/72c016027c55d18dc3e1daac934244ac.png)
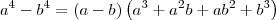


emsbp escreveu:Agora a dúvida é como chegou à expressão que diz que tenho que multiplicar ao numerador e ao denominador.
![\sqrt[4]{x+h}-\sqrt[4]{x} \sqrt[4]{x+h}-\sqrt[4]{x}](/latexrender/pictures/a17d9920a84610f95155bf97f59bb30a.png)
![\left(\sqrt[4]{x+h}\right)^4- \left(\sqrt[4]{x}\right)^4 \left(\sqrt[4]{x+h}\right)^4- \left(\sqrt[4]{x}\right)^4](/latexrender/pictures/7944cc1d9e586762d98a12b57afecaaa.png)
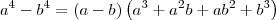
![a =\sqrt[4]{x+h} a =\sqrt[4]{x+h}](/latexrender/pictures/b99ecc8215c4d73e13163d6b7ee28426.png)
![b =\sqrt[4]{x} b =\sqrt[4]{x}](/latexrender/pictures/61b265ca748d56b0dfc9c405b1e5a8fa.png)
![\left(\sqrt[4]{x+h}\right)^4- \left(\sqrt[4]{x}\right)^4 \left(\sqrt[4]{x+h}\right)^4- \left(\sqrt[4]{x}\right)^4](/latexrender/pictures/7944cc1d9e586762d98a12b57afecaaa.png)
![\,= \left(\sqrt[4]{x+h} - \sqrt[4]{x}\right)\left[\left(\sqrt[4]{x+h}\right)^3 + \left(\sqrt[4]{x+h}\right)^2\left(\sqrt[4]{x}\right) + \left(\sqrt[4]{x+h}\right)\left(\sqrt[4]{x}\right)^2 + \left(\sqrt[4]{x}\right)^3\right] \,= \left(\sqrt[4]{x+h} - \sqrt[4]{x}\right)\left[\left(\sqrt[4]{x+h}\right)^3 + \left(\sqrt[4]{x+h}\right)^2\left(\sqrt[4]{x}\right) + \left(\sqrt[4]{x+h}\right)\left(\sqrt[4]{x}\right)^2 + \left(\sqrt[4]{x}\right)^3\right]](/latexrender/pictures/56399eadfd7ef352e099335ff672ec02.png)


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)