 por emsbp » Qua Mai 02, 2012 10:34
por emsbp » Qua Mai 02, 2012 10:34
Bom dia.
Peço ajuda no cálculo da derivada, pela definição, da função
![\sqrt[4]{x} \sqrt[4]{x}](/latexrender/pictures/c0e46d4c908766f6783b14291952c9c5.png)
.
Comecei por
![\lim_{h\rightarrow0}\frac{\sqrt[4]{x+h}-\sqrt[4]{x}}{h} \lim_{h\rightarrow0}\frac{\sqrt[4]{x+h}-\sqrt[4]{x}}{h}](/latexrender/pictures/6dcfefa247ee0971143234d435710008.png)
. Depois tentei ir desenvolver, aplicando o conjugado do numerador, mas a partir daí não consegui avançar.
Obrigado!
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por LuizAquino » Qua Mai 02, 2012 13:55
por LuizAquino » Qua Mai 02, 2012 13:55
emsbp escreveu:Peço ajuda no cálculo da derivada, pela definição, da função
![\sqrt[4]{x} \sqrt[4]{x}](/latexrender/pictures/c0e46d4c908766f6783b14291952c9c5.png)
.
Comecei por
![\lim_{h\rightarrow0}\frac{\sqrt[4]{x+h}-\sqrt[4]{x}}{h} \lim_{h\rightarrow0}\frac{\sqrt[4]{x+h}-\sqrt[4]{x}}{h}](/latexrender/pictures/6dcfefa247ee0971143234d435710008.png)
. Depois tentei ir desenvolver, aplicando o conjugado do numerador, mas a partir daí não consegui avançar.
O seu erro foi multiplicar pelo "conjugado".
O você precisa fazer é multiplicar o numerador e o denominador por:
![\left[\left(\sqrt[4]{x+h}\right)^3 + \left(\sqrt[4]{x+h}\right)^2\left(\sqrt[4]{x}\right) + \left(\sqrt[4]{x+h}\right)\left(\sqrt[4]{x}\right)^2 + \left(\sqrt[4]{x}\right)^3\right] \left[\left(\sqrt[4]{x+h}\right)^3 + \left(\sqrt[4]{x+h}\right)^2\left(\sqrt[4]{x}\right) + \left(\sqrt[4]{x+h}\right)\left(\sqrt[4]{x}\right)^2 + \left(\sqrt[4]{x}\right)^3\right]](/latexrender/pictures/72c016027c55d18dc3e1daac934244ac.png)
Em seguida, no numerador use o seguinte produto notável:
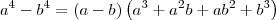
Agora tente continuar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por emsbp » Qua Mai 02, 2012 14:23
por emsbp » Qua Mai 02, 2012 14:23
Boa tarde.
Ok. Obrigado.
Agora a dúvida é como chegou à expressão que diz que tenho que multiplicar ao numerador e ao denominador.
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por LuizAquino » Qua Mai 02, 2012 14:40
por LuizAquino » Qua Mai 02, 2012 14:40
emsbp escreveu:Agora a dúvida é como chegou à expressão que diz que tenho que multiplicar ao numerador e ao denominador.
Você chega nessa expressão ao analisar o produto notável.
Note que o numerador da fração era
![\sqrt[4]{x+h}-\sqrt[4]{x} \sqrt[4]{x+h}-\sqrt[4]{x}](/latexrender/pictures/a17d9920a84610f95155bf97f59bb30a.png)
Para eliminar essa raiz quarta, precisamos elevar a quarta potência. Ou seja, precisamos fazer aparecer algo como:
![\left(\sqrt[4]{x+h}\right)^4- \left(\sqrt[4]{x}\right)^4 \left(\sqrt[4]{x+h}\right)^4- \left(\sqrt[4]{x}\right)^4](/latexrender/pictures/7944cc1d9e586762d98a12b57afecaaa.png)
Para fazer essa expressão aparecer, devemos lembrar do produto notável indicado anteriormente:
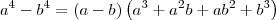
Comparando esse produto notável com a expressão que desejamos fazer aparecer, basta fixar:
![a =\sqrt[4]{x+h} a =\sqrt[4]{x+h}](/latexrender/pictures/b99ecc8215c4d73e13163d6b7ee28426.png)
![b =\sqrt[4]{x} b =\sqrt[4]{x}](/latexrender/pictures/61b265ca748d56b0dfc9c405b1e5a8fa.png)
Ou seja, temos que:
![\left(\sqrt[4]{x+h}\right)^4- \left(\sqrt[4]{x}\right)^4 \left(\sqrt[4]{x+h}\right)^4- \left(\sqrt[4]{x}\right)^4](/latexrender/pictures/7944cc1d9e586762d98a12b57afecaaa.png)
![\,= \left(\sqrt[4]{x+h} - \sqrt[4]{x}\right)\left[\left(\sqrt[4]{x+h}\right)^3 + \left(\sqrt[4]{x+h}\right)^2\left(\sqrt[4]{x}\right) + \left(\sqrt[4]{x+h}\right)\left(\sqrt[4]{x}\right)^2 + \left(\sqrt[4]{x}\right)^3\right] \,= \left(\sqrt[4]{x+h} - \sqrt[4]{x}\right)\left[\left(\sqrt[4]{x+h}\right)^3 + \left(\sqrt[4]{x+h}\right)^2\left(\sqrt[4]{x}\right) + \left(\sqrt[4]{x+h}\right)\left(\sqrt[4]{x}\right)^2 + \left(\sqrt[4]{x}\right)^3\right]](/latexrender/pictures/56399eadfd7ef352e099335ff672ec02.png)
Daí concluímos que precisamos multiplicar o numerador e o denominador da fração no limite pela expressão indicada anteriormente.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por emsbp » Qua Mai 02, 2012 18:11
por emsbp » Qua Mai 02, 2012 18:11
Muito obrigado.
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada pela Definiçao
por PeIdInHu » Sáb Mai 22, 2010 17:24
- 1 Respostas
- 2205 Exibições
- Última mensagem por admin

Sáb Mai 22, 2010 18:24
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela definiçao
por tumiattibrz » Sex Mai 27, 2011 17:17
- 3 Respostas
- 2518 Exibições
- Última mensagem por LuizAquino

Sáb Mai 28, 2011 12:28
Cálculo: Limites, Derivadas e Integrais
-
- derivada pela definiçao
por paula luna » Sex Jun 10, 2011 04:41
- 2 Respostas
- 2287 Exibições
- Última mensagem por Fabio Cabral

Sex Jun 10, 2011 11:23
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela definição
por core » Qua Out 16, 2013 02:15
- 1 Respostas
- 1758 Exibições
- Última mensagem por Taka

Sáb Nov 02, 2013 21:26
Cálculo: Limites, Derivadas e Integrais
-
- derivada pela definição
 por JoaoLuiz07 » Ter Fev 02, 2016 10:02
por JoaoLuiz07 » Ter Fev 02, 2016 10:02
- 1 Respostas
- 1703 Exibições
- Última mensagem por adauto martins

Qui Fev 04, 2016 15:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[4]{x} \sqrt[4]{x}](/latexrender/pictures/c0e46d4c908766f6783b14291952c9c5.png) .
.![\lim_{h\rightarrow0}\frac{\sqrt[4]{x+h}-\sqrt[4]{x}}{h} \lim_{h\rightarrow0}\frac{\sqrt[4]{x+h}-\sqrt[4]{x}}{h}](/latexrender/pictures/6dcfefa247ee0971143234d435710008.png) . Depois tentei ir desenvolver, aplicando o conjugado do numerador, mas a partir daí não consegui avançar.
. Depois tentei ir desenvolver, aplicando o conjugado do numerador, mas a partir daí não consegui avançar.
![\sqrt[4]{x} \sqrt[4]{x}](/latexrender/pictures/c0e46d4c908766f6783b14291952c9c5.png) .
.![\lim_{h\rightarrow0}\frac{\sqrt[4]{x+h}-\sqrt[4]{x}}{h} \lim_{h\rightarrow0}\frac{\sqrt[4]{x+h}-\sqrt[4]{x}}{h}](/latexrender/pictures/6dcfefa247ee0971143234d435710008.png) . Depois tentei ir desenvolver, aplicando o conjugado do numerador, mas a partir daí não consegui avançar.
. Depois tentei ir desenvolver, aplicando o conjugado do numerador, mas a partir daí não consegui avançar.
.
. Depois tentei ir desenvolver, aplicando o conjugado do numerador, mas a partir daí não consegui avançar.
![\left[\left(\sqrt[4]{x+h}\right)^3 + \left(\sqrt[4]{x+h}\right)^2\left(\sqrt[4]{x}\right) + \left(\sqrt[4]{x+h}\right)\left(\sqrt[4]{x}\right)^2 + \left(\sqrt[4]{x}\right)^3\right] \left[\left(\sqrt[4]{x+h}\right)^3 + \left(\sqrt[4]{x+h}\right)^2\left(\sqrt[4]{x}\right) + \left(\sqrt[4]{x+h}\right)\left(\sqrt[4]{x}\right)^2 + \left(\sqrt[4]{x}\right)^3\right]](/latexrender/pictures/72c016027c55d18dc3e1daac934244ac.png)
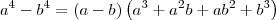


![\sqrt[4]{x+h}-\sqrt[4]{x} \sqrt[4]{x+h}-\sqrt[4]{x}](/latexrender/pictures/a17d9920a84610f95155bf97f59bb30a.png)
![\left(\sqrt[4]{x+h}\right)^4- \left(\sqrt[4]{x}\right)^4 \left(\sqrt[4]{x+h}\right)^4- \left(\sqrt[4]{x}\right)^4](/latexrender/pictures/7944cc1d9e586762d98a12b57afecaaa.png)
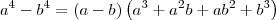
![a =\sqrt[4]{x+h} a =\sqrt[4]{x+h}](/latexrender/pictures/b99ecc8215c4d73e13163d6b7ee28426.png)
![b =\sqrt[4]{x} b =\sqrt[4]{x}](/latexrender/pictures/61b265ca748d56b0dfc9c405b1e5a8fa.png)
![\left(\sqrt[4]{x+h}\right)^4- \left(\sqrt[4]{x}\right)^4 \left(\sqrt[4]{x+h}\right)^4- \left(\sqrt[4]{x}\right)^4](/latexrender/pictures/7944cc1d9e586762d98a12b57afecaaa.png)
![\,= \left(\sqrt[4]{x+h} - \sqrt[4]{x}\right)\left[\left(\sqrt[4]{x+h}\right)^3 + \left(\sqrt[4]{x+h}\right)^2\left(\sqrt[4]{x}\right) + \left(\sqrt[4]{x+h}\right)\left(\sqrt[4]{x}\right)^2 + \left(\sqrt[4]{x}\right)^3\right] \,= \left(\sqrt[4]{x+h} - \sqrt[4]{x}\right)\left[\left(\sqrt[4]{x+h}\right)^3 + \left(\sqrt[4]{x+h}\right)^2\left(\sqrt[4]{x}\right) + \left(\sqrt[4]{x+h}\right)\left(\sqrt[4]{x}\right)^2 + \left(\sqrt[4]{x}\right)^3\right]](/latexrender/pictures/56399eadfd7ef352e099335ff672ec02.png)

