 por moyses » Ter Mai 01, 2012 20:50
por moyses » Ter Mai 01, 2012 20:50
Olá gente beleza? Eu estava estudando teoria de conjuntos no Livro de Matemática "MATEMÀTICA AULA POR AULA", de Benigno Barreto Filho e Cláudio Xavier da Silva. Cheguei numa pergunta que não consigui interpreta-la .A minha duvida é de o que o problema ta querendo dizer? e como provar o que diz nessa pergunta 43 contida na pagina 38 desse livro que eu mencione acima?.
Bem Ai vai:
43 (ITA-SP) Sejam
U um conjunto não-vazio e
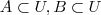
. Usando apenas as definições de igualdade, reunião, intercecção e complementar, prove que:
I- SE
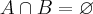
, então
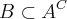
.
II-SE
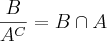
.
e ai que está , gente eu nem sei como começar. O que o item
II ta querendo dizer? e como provar o item
I e o
II? por favor me ajudem pois eu tentei e não consegui!

 PS-
PS- essa
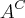
e o complemento do próprio conjunto, eu dei uma pesquisada na net porque eu tabem não sabia hehe. e o item dois tem um divisão do conjunto B pelo complemento do proprio conjunto A ? e isso mesmo? fica a duvida! falow desde já eu agradeço a todos faloww pessoal!

-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por fraol » Ter Mai 01, 2012 22:52
por fraol » Ter Mai 01, 2012 22:52
Boa noite,
Segue a minha resolução para sua avaliação:
I) Como
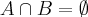
temos que se

. (editei aqui p/ corrigir digitação)
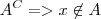
. Assim concluímos que
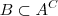
.
II)Suponho que a notação seja
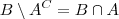
. Aqui
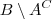
significa

menos
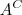
, ou seja o conjunto dos elementos que estão em

e não estão em
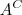
.
Assim
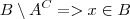
e
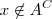
.
Como em
I) temos que todo

em

também está em
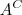
então
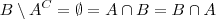
.
.
Editado pela última vez por
fraol em Ter Mai 01, 2012 23:54, em um total de 1 vez.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por moyses » Ter Mai 01, 2012 23:37
por moyses » Ter Mai 01, 2012 23:37
Teria com você exclicar melhor é por que é meio estrainho isso. Se a intersecção de A com B é igual a vazio como B estaria contido no conjunto complementar de A no Item I?
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por fraol » Ter Mai 01, 2012 23:49
por fraol » Ter Mai 01, 2012 23:49
Se a interseção de A com B é vazia então A e B não tem elementos em comum, certo?
O complementar de A são todos os elementos do conjunto Universo que não estão em A, certo?
Se os elementos de B não estão em A então estão no complementar de A.
Caso a dúvida permaneça manda de volta pra gente discutir.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por moyses » Qua Mai 02, 2012 10:08
por moyses » Qua Mai 02, 2012 10:08
Ahh entendi ! eu pensava que a complementar do proprio A seria

só que eu me enganei, como no enunciado diz que
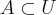
e tambem que
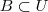
então no
Item
I e no
II dois fica assim:(Explicarei como eu entendi heheh

)
I- SE
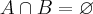
, então como
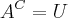
então
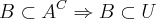
então como
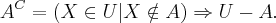
então o que você me falou é verdade que o
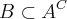
. Agora que eu entendi e compreendi. Agora o item
II ficou mais facil de entender.
II- SE
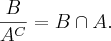
então como
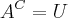
então
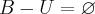
e como a

ou
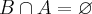
eu entendi que essa igualdade é verdadeira !!!
VALEWW Por me exclicar direitinho fraol . Fica com DEUS

!
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Problema de conjuntos com porcentagem
por Tibes » Qui Jan 31, 2013 14:29
- 1 Respostas
- 7959 Exibições
- Última mensagem por young_jedi

Sex Fev 01, 2013 12:39
Conjuntos
-
- Demostração
por Balanar » Dom Ago 29, 2010 05:43
- 1 Respostas
- 951 Exibições
- Última mensagem por Douglasm

Dom Ago 29, 2010 15:56
Álgebra Elementar
-
- Demostração da Regra do Trapézio
por ARCS » Sex Fev 10, 2012 19:12
- 1 Respostas
- 1182 Exibições
- Última mensagem por LuizAquino

Sáb Fev 11, 2012 11:34
Cálculo: Limites, Derivadas e Integrais
-
- Demostração das identidades trigonometricas
por Alerecife » Sáb Set 08, 2012 13:32
- 3 Respostas
- 1939 Exibições
- Última mensagem por MarceloFantini

Dom Set 09, 2012 17:45
Trigonometria
-
- Sistemas Lineares e demostração de LI e LD?
por Alerecife » Sáb Abr 27, 2013 22:57
- 1 Respostas
- 7039 Exibições
- Última mensagem por Alerecife

Ter Abr 30, 2013 23:16
Álgebra
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
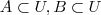 . Usando apenas as definições de igualdade, reunião, intercecção e complementar, prove que:
. Usando apenas as definições de igualdade, reunião, intercecção e complementar, prove que: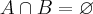 , então
, então 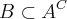 .
.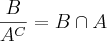 .
.

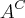 e o complemento do próprio conjunto, eu dei uma pesquisada na net porque eu tabem não sabia hehe. e o item dois tem um divisão do conjunto B pelo complemento do proprio conjunto A ? e isso mesmo? fica a duvida! falow desde já eu agradeço a todos faloww pessoal!
e o complemento do próprio conjunto, eu dei uma pesquisada na net porque eu tabem não sabia hehe. e o item dois tem um divisão do conjunto B pelo complemento do proprio conjunto A ? e isso mesmo? fica a duvida! falow desde já eu agradeço a todos faloww pessoal! 


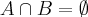 temos que se
temos que se  . (editei aqui p/ corrigir digitação)
. (editei aqui p/ corrigir digitação)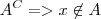 . Assim concluímos que
. Assim concluímos que 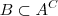 .
.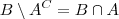 . Aqui
. Aqui 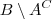 significa
significa  menos
menos 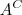 , ou seja o conjunto dos elementos que estão em
, ou seja o conjunto dos elementos que estão em 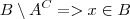 e
e 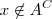 .
. em
em 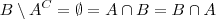 .
.
 só que eu me enganei, como no enunciado diz que
só que eu me enganei, como no enunciado diz que 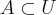 e tambem que
e tambem que 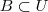 então no
então no 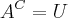 então
então 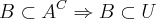 então como
então como 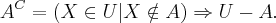 então o que você me falou é verdade que o
então o que você me falou é verdade que o 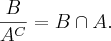 então como
então como 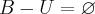 e como a
e como a  ou
ou 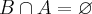 eu entendi que essa igualdade é verdadeira !!!
eu entendi que essa igualdade é verdadeira !!!