 por Fiel8 » Qua Jul 01, 2009 17:29
por Fiel8 » Qua Jul 01, 2009 17:29
Esse exercicio como é :determine o(s) zero(s) ou a(s) raiz(es) das seguintes funçoes quadraticas:
f(x)=xelevado a 2-4, f(x)=xelevado a 2+2x, f(x)=xelevado a 2-6x+9, f(x)=xelevado a 2-10x+16 ...
-
Fiel8
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Ter Jun 16, 2009 17:21
- Formação Escolar: EJA
- Andamento: cursando
 por Molina » Qua Jul 01, 2009 20:49
por Molina » Qua Jul 01, 2009 20:49
Fiel, por favor, crie os tópicos
usando títulos ligados a sua dúvida, ok?
Quanto a sua questão você quer saber o seguinte:
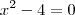
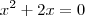
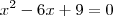
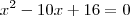
Ou seja, você quer saber os valores de x para que o lado esquerdo da igualdade seja igual a ZERO.
A primeira e a segunda, são casos em que a equação do 2º grau está incompleta. Há certos modos de faze-las. As duas últimas são equações do 2º grau completas, em que você deve utilizar a Fórmula de Bháskara para achas as soluções.
Consegue resolve-las sozinho? Exponha suas dúvidas.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Sex Jul 03, 2009 12:19
por Cleyson007 » Sex Jul 03, 2009 12:19
Bom dia Fiel8!
A explicação do Molina foi muito boa

Para calcular o valor de

, faça o seguinte:
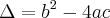
.
Quanto ao valor de Bháskara:
![\frac{-b{+}_{-}\sqrt[2]{\Delta}}{2a} \frac{-b{+}_{-}\sqrt[2]{\Delta}}{2a}](/latexrender/pictures/a5f899a48af422cd544594f88cab7fcd.png)
.
Comente qualquer dúvida,

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



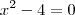
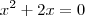
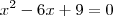
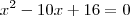



 , faça o seguinte:
, faça o seguinte: 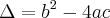 .
.![\frac{-b{+}_{-}\sqrt[2]{\Delta}}{2a} \frac{-b{+}_{-}\sqrt[2]{\Delta}}{2a}](/latexrender/pictures/a5f899a48af422cd544594f88cab7fcd.png) .
.
