 por Fiel8 » Qua Jul 01, 2009 17:29
por Fiel8 » Qua Jul 01, 2009 17:29
Esse exercicio como é :determine o(s) zero(s) ou a(s) raiz(es) das seguintes funçoes quadraticas:
f(x)=xelevado a 2-4, f(x)=xelevado a 2+2x, f(x)=xelevado a 2-6x+9, f(x)=xelevado a 2-10x+16 ...
-
Fiel8
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Ter Jun 16, 2009 17:21
- Formação Escolar: EJA
- Andamento: cursando
 por Molina » Qua Jul 01, 2009 20:49
por Molina » Qua Jul 01, 2009 20:49
Fiel, por favor, crie os tópicos
usando títulos ligados a sua dúvida, ok?
Quanto a sua questão você quer saber o seguinte:
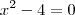
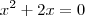
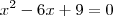
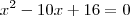
Ou seja, você quer saber os valores de x para que o lado esquerdo da igualdade seja igual a ZERO.
A primeira e a segunda, são casos em que a equação do 2º grau está incompleta. Há certos modos de faze-las. As duas últimas são equações do 2º grau completas, em que você deve utilizar a Fórmula de Bháskara para achas as soluções.
Consegue resolve-las sozinho? Exponha suas dúvidas.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Sex Jul 03, 2009 12:19
por Cleyson007 » Sex Jul 03, 2009 12:19
Bom dia Fiel8!
A explicação do Molina foi muito boa

Para calcular o valor de

, faça o seguinte:
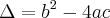
.
Quanto ao valor de Bháskara:
![\frac{-b{+}_{-}\sqrt[2]{\Delta}}{2a} \frac{-b{+}_{-}\sqrt[2]{\Delta}}{2a}](/latexrender/pictures/a5f899a48af422cd544594f88cab7fcd.png)
.
Comente qualquer dúvida,

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



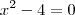
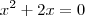
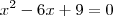
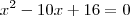



 , faça o seguinte:
, faça o seguinte: 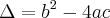 .
.![\frac{-b{+}_{-}\sqrt[2]{\Delta}}{2a} \frac{-b{+}_{-}\sqrt[2]{\Delta}}{2a}](/latexrender/pictures/a5f899a48af422cd544594f88cab7fcd.png) .
.






