 por jvabatista » Qua Abr 18, 2012 01:42
por jvabatista » Qua Abr 18, 2012 01:42
Olá.
Estou com problemas para resolver isto:
![\frac{8{x}^{\frac{3}{5}}-2\sqrt[3]{{x}^{2}}+{x}^{\frac{4}{5}}}{\sqrt[2]{{x}^{5}}} \frac{8{x}^{\frac{3}{5}}-2\sqrt[3]{{x}^{2}}+{x}^{\frac{4}{5}}}{\sqrt[2]{{x}^{5}}}](/latexrender/pictures/e143555ff719c2230efe0af738ac184b.png)
**Divida, deixando aparecer somente expoentes positivos
Separei cada membro de cima com o mesmo denominador, dividi cada um dos três separadamente e encontrei isto:
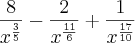
Não sei como simplificar mais do que isso e a resposta no livro é
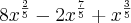
.
Tentei resolver pelo método das chaves mas obtive o mesmo resultado. Há algum outro método para se chegar ao resultado do livro ou algo mais a simplificar de até onde calculei ?
-
jvabatista
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Abr 16, 2012 22:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por DanielFerreira » Qua Abr 18, 2012 23:08
por DanielFerreira » Qua Abr 18, 2012 23:08
![\frac{8x^{\frac{3}{5}} - 2\sqrt[3]{x^2} + x^{\frac{4}{5}}}{\sqrt[]{x^5}} = \frac{8x^{\frac{3}{5}} - 2\sqrt[3]{x^2} + x^{\frac{4}{5}}}{\sqrt[]{x^5}} =](/latexrender/pictures/1a18ed8f0b2fb137f222168efa9eb9b5.png)
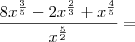
Aplicando MMC vamos deixar os denominadores iguais:
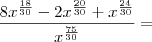
Acho que agora vc consegue, tente!
Qualquer dúvida retorne.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por jvabatista » Qui Abr 26, 2012 17:49
por jvabatista » Qui Abr 26, 2012 17:49
Oi, tentei resolver aplicando o MMC, da mesma forma que fiz o anterior - separei cada termo com seu denominador -, ficando:
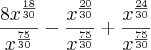
.
Mas ainda continuo obtendo o mesmo resultado de anteriormente. Há outro meio de seguir a equação que não seja este que utilizei ?
-
jvabatista
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Abr 16, 2012 22:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por DanielFerreira » Qui Abr 26, 2012 20:13
por DanielFerreira » Qui Abr 26, 2012 20:13
jvabatista escreveu:Oi, tentei resolver aplicando o MMC, da mesma forma que fiz o anterior - separei cada termo com seu denominador -, ficando:
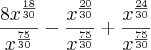
.
Mas ainda continuo obtendo o mesmo resultado de anteriormente. Há outro meio de seguir a equação que não seja este que utilizei ?
Você esqueceu de colocar o 2 (termo negativo).
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por jvabatista » Qui Abr 26, 2012 20:52
por jvabatista » Qui Abr 26, 2012 20:52
Desculpe, é verdade. Esqueci o 2 quando digitei a expressão. Mas ela continua dando o mesmo resultado.
-
jvabatista
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Abr 16, 2012 22:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por DanielFerreira » Qui Abr 26, 2012 21:15
por DanielFerreira » Qui Abr 26, 2012 21:15
jvabatista escreveu:Desculpe, é verdade. Esqueci o 2 quando digitei a expressão. Mas ela continua dando o mesmo resultado.
Então vamos a ela.
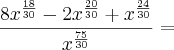
Pelo que entendi até aqui tudo bem, certo?!
Então, coloque
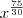
em evidência, veja:
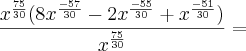
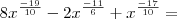
ou
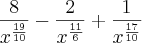
também encontrou isso?
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por jvabatista » Qui Abr 26, 2012 21:27
por jvabatista » Qui Abr 26, 2012 21:27
Sim. Então a resposta do livro tá errada mesmo né? rsrs. Muito obrigado.
-
jvabatista
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Abr 16, 2012 22:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por DanielFerreira » Dom Abr 29, 2012 00:42
por DanielFerreira » Dom Abr 29, 2012 00:42
jvabatista escreveu:Sim. Então a resposta do livro tá errada mesmo né? rsrs. Muito obrigado.
De acordo!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- fatoração de polinomios
por theSinister » Ter Mai 10, 2011 20:23
- 1 Respostas
- 1771 Exibições
- Última mensagem por MarceloFantini

Ter Mai 10, 2011 21:33
Álgebra Elementar
-
- [Polinomios] Fatoração
por carvalhothg » Ter Set 20, 2011 18:08
- 3 Respostas
- 1969 Exibições
- Última mensagem por MarceloFantini

Ter Set 20, 2011 19:19
Polinômios
-
- Fatoração de polinômios
por Danilo » Sáb Jul 28, 2012 12:45
- 2 Respostas
- 1698 Exibições
- Última mensagem por Danilo

Sáb Jul 28, 2012 14:03
Polinômios
-
- Fatoração de polinômios
por Danilo » Sex Ago 16, 2013 16:51
- 3 Respostas
- 2356 Exibições
- Última mensagem por Danilo

Sex Ago 16, 2013 18:16
Polinômios
-
- Fatoração de Polinômios
por matheus_frs1 » Sex Mar 18, 2016 22:49
- 1 Respostas
- 1979 Exibições
- Última mensagem por DanielFerreira

Sáb Jul 16, 2016 23:08
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{8{x}^{\frac{3}{5}}-2\sqrt[3]{{x}^{2}}+{x}^{\frac{4}{5}}}{\sqrt[2]{{x}^{5}}} \frac{8{x}^{\frac{3}{5}}-2\sqrt[3]{{x}^{2}}+{x}^{\frac{4}{5}}}{\sqrt[2]{{x}^{5}}}](/latexrender/pictures/e143555ff719c2230efe0af738ac184b.png)
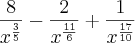
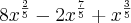 .
.

![\frac{8x^{\frac{3}{5}} - 2\sqrt[3]{x^2} + x^{\frac{4}{5}}}{\sqrt[]{x^5}} = \frac{8x^{\frac{3}{5}} - 2\sqrt[3]{x^2} + x^{\frac{4}{5}}}{\sqrt[]{x^5}} =](/latexrender/pictures/1a18ed8f0b2fb137f222168efa9eb9b5.png)
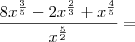
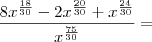

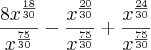 .
.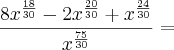
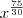 em evidência, veja:
em evidência, veja: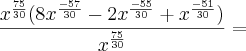
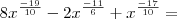
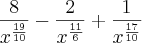


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.