 por Andrewo » Qui Abr 19, 2012 14:05
por Andrewo » Qui Abr 19, 2012 14:05
Aí pessoal , blza? Algumas dúvidazinhas aí sobre radicais
Nessa pra simplificar, meu resultado não bateu
![\sqrt[12]{{2}^{3}.{a}^{6}} \sqrt[12]{{2}^{3}.{a}^{6}}](/latexrender/pictures/2132be55b04d27134c15735f3bd39d1f.png)
Simplificando fica:
=
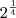
e
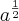
Aí então não ficariam em raízes separadas já que o indicador mudou? =
![\sqrt[4]{2} \sqrt[4]{2}](/latexrender/pictures/2f92f26b5ec4b063312e1be4bafd7452.png)
e
![\sqrt[]{a} \sqrt[]{a}](/latexrender/pictures/3d48e387f88a173a4e4cf3b38dbab4a6.png)
Pq o resultado fica
![\sqrt[4]{2.{a}^{2}} \sqrt[4]{2.{a}^{2}}](/latexrender/pictures/ce73b25dcff3d2c7167d63e5e79adcf9.png)
????
2-
![{(1-\sqrt[]{2})}^{2} {(1-\sqrt[]{2})}^{2}](/latexrender/pictures/064ba63db0deade10f842f254c26b8dc.png)
![(3-\sqrt[]{2}) (3-\sqrt[]{2})](/latexrender/pictures/65e7f9b3a3917d9ea8cd8e3083e426fa.png)
Como eu fiz :
![(3-\sqrt[]{2})(3-\sqrt[]{2}) (3-\sqrt[]{2})(3-\sqrt[]{2})](/latexrender/pictures/58f7576051e80abb42df2fce604d58aa.png)
=
![9-12\sqrt[]{2} + 8 = 17-12\sqrt[]{2} 9-12\sqrt[]{2} + 8 = 17-12\sqrt[]{2}](/latexrender/pictures/280d932b46b0639153364cdd24ff81b8.png)
Resultado pelo gabarito : 1
3 -
![\frac{a-b}{\sqrt[]{a}-\sqrt[]{b}} \frac{a-b}{\sqrt[]{a}-\sqrt[]{b}}](/latexrender/pictures/adcfd5a77f7da6b1e6ac10b12505fc59.png)
b
Como eu fiz :
![\frac{a-b}{\sqrt[]{a}-\sqrt[]{b}}.\frac{\sqrt[]{a}+\sqrt[]{b}}{\sqrt[]{a}+\sqrt[]{b}} \frac{a-b}{\sqrt[]{a}-\sqrt[]{b}}.\frac{\sqrt[]{a}+\sqrt[]{b}}{\sqrt[]{a}+\sqrt[]{b}}](/latexrender/pictures/4a80b60f385b88a718fa9bbdfb1e334e.png)
=
![\frac{a\sqrt[]{a}+a\sqrt[]{b}-b\sqrt[]{a}-b\sqrt[]{b}}{a-b} \frac{a\sqrt[]{a}+a\sqrt[]{b}-b\sqrt[]{a}-b\sqrt[]{b}}{a-b}](/latexrender/pictures/d44e9bbebb6c4a01f2288595c3a64731.png)
«
Resultado pelo gabarito :
![\sqrt[]{a}+\sqrt[]{b} \sqrt[]{a}+\sqrt[]{b}](/latexrender/pictures/17957293567ab489803a1248360d8334.png)



-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Sáb Abr 21, 2012 13:46
por DanielFerreira » Sáb Abr 21, 2012 13:46
Andrewo escreveu:Aí pessoal , blza? Algumas dúvidazinhas aí sobre radicais
Nessa pra simplificar, meu resultado não bateu
![\sqrt[12]{{2}^{3}.{a}^{6}} \sqrt[12]{{2}^{3}.{a}^{6}}](/latexrender/pictures/2132be55b04d27134c15735f3bd39d1f.png)
Simplificando fica:
=
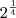
e
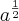
Aí então não ficariam em raízes separadas já que o indicador mudou? =
![\sqrt[4]{2} \sqrt[4]{2}](/latexrender/pictures/2f92f26b5ec4b063312e1be4bafd7452.png)
e
![\sqrt[]{a} \sqrt[]{a}](/latexrender/pictures/3d48e387f88a173a4e4cf3b38dbab4a6.png)
Pq o resultado fica
![\sqrt[4]{2.{a}^{2}} \sqrt[4]{2.{a}^{2}}](/latexrender/pictures/ce73b25dcff3d2c7167d63e5e79adcf9.png)
????
![\sqrt[12]{2^3.a^6} = \sqrt[12]{2^3.a^6} =](/latexrender/pictures/61c755686471832d3ae75f87ff57e5bb.png)
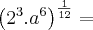
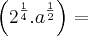
![\sqrt[4]{2} . \sqrt[]{a} = \sqrt[4]{2} . \sqrt[]{a} =](/latexrender/pictures/60049d51c311b108664f5f6a26ca8674.png)
Parece que seu raciocínio foi esse, e está correto!
Só que não acaba por aqui, deverá colocá-los numa raiz.
![\sqrt[n]{x} \sqrt[n]{x}](/latexrender/pictures/13fcbed8bcac58d95c0cb989f3aca2de.png)
n ---> índice
x ---> radicando
Tire o MMC entre os índices das raízes;
Divida o MMC pelos índices, o resultado será o expoente do radicando.
continuando...
![\sqrt[4]{2} . \sqrt[]{a} = \sqrt[4]{2} . \sqrt[]{a} =](/latexrender/pictures/60049d51c311b108664f5f6a26ca8674.png)
![\sqrt[4]{2} . \sqrt[4]{a^2} = \sqrt[4]{2} . \sqrt[4]{a^2} =](/latexrender/pictures/fb4f6f82d647fbd97a0dcf9cff77a778.png)
![\sqrt[4]{2.a^2} \sqrt[4]{2.a^2}](/latexrender/pictures/d81727c89e463f38666e8a3633fe55d0.png)
Vale destacar que só poderá multiplicar os radicandos com estes estiverem sob raízes de mesmo índice.
Espero ter ajudado!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Sáb Abr 21, 2012 13:55
por DanielFerreira » Sáb Abr 21, 2012 13:55
Andrewo escreveu:Aí pessoal , blza? Algumas dúvidazinhas aí sobre radicais
2-
![{(1-\sqrt[]{2})}^{2} {(1-\sqrt[]{2})}^{2}](/latexrender/pictures/064ba63db0deade10f842f254c26b8dc.png)
![(3-\sqrt[]{2}) (3-\sqrt[]{2})](/latexrender/pictures/65e7f9b3a3917d9ea8cd8e3083e426fa.png)
Como eu fiz :
![(3-\sqrt[]{2})(3-\sqrt[]{2}) (3-\sqrt[]{2})(3-\sqrt[]{2})](/latexrender/pictures/58f7576051e80abb42df2fce604d58aa.png)
=
![9-12\sqrt[]{2} + 8 = 17-12\sqrt[]{2} 9-12\sqrt[]{2} + 8 = 17-12\sqrt[]{2}](/latexrender/pictures/280d932b46b0639153364cdd24ff81b8.png)
Resultado pelo gabarito : 1
![(1 - \sqrt[]{2})^2(3 - \sqrt[]{2}) = (1 - \sqrt[]{2})^2(3 - \sqrt[]{2}) =](/latexrender/pictures/8077873616e12b369d8ea4e305d67eb8.png)
![(1 - 2\sqrt[]{2} + 2)(3 - \sqrt[]{2}) = (1 - 2\sqrt[]{2} + 2)(3 - \sqrt[]{2}) =](/latexrender/pictures/c67779cec3dba68dbec8b388ecc68b8c.png)
![(3 - 2\sqrt[]{2})(3 - \sqrt[]{2}) = (3 - 2\sqrt[]{2})(3 - \sqrt[]{2}) =](/latexrender/pictures/ffa52ccb838ed4a12b592d69214cce51.png)
Observe que:
![(3 - 2\sqrt[]{2}) \neq(3 - \sqrt[]{2}) (3 - 2\sqrt[]{2}) \neq(3 - \sqrt[]{2})](/latexrender/pictures/25aad3d31e331c1175a7084b93886e4c.png)
então não pode elevá-los ao quadrado, só poderá fazer isso se forem
iguais.
Aplique distributiva, veja:
![(3 - 2\sqrt[]{2})(3 - \sqrt[]{2}) = (3 - 2\sqrt[]{2})(3 - \sqrt[]{2}) =](/latexrender/pictures/ffa52ccb838ed4a12b592d69214cce51.png)
![9 - 3\sqrt[]{2} - 6\sqrt[]{2} + 4 = 9 - 3\sqrt[]{2} - 6\sqrt[]{2} + 4 =](/latexrender/pictures/0de36282adb00ba1ef22579cfa05267c.png)
![13 - 9\sqrt[]{2} 13 - 9\sqrt[]{2}](/latexrender/pictures/0a7db61fc6505df805c802fa52f8746d.png)
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Sáb Abr 21, 2012 14:01
por DanielFerreira » Sáb Abr 21, 2012 14:01
Andrewo escreveu:Aí pessoal , blza? Algumas dúvidazinhas aí sobre radicais
3 -
![\frac{a-b}{\sqrt[]{a}-\sqrt[]{b}} \frac{a-b}{\sqrt[]{a}-\sqrt[]{b}}](/latexrender/pictures/adcfd5a77f7da6b1e6ac10b12505fc59.png)
b
Como eu fiz :
![\frac{a-b}{\sqrt[]{a}-\sqrt[]{b}}.\frac{\sqrt[]{a}+\sqrt[]{b}}{\sqrt[]{a}+\sqrt[]{b}} \frac{a-b}{\sqrt[]{a}-\sqrt[]{b}}.\frac{\sqrt[]{a}+\sqrt[]{b}}{\sqrt[]{a}+\sqrt[]{b}}](/latexrender/pictures/4a80b60f385b88a718fa9bbdfb1e334e.png)
=
![\frac{a\sqrt[]{a}+a\sqrt[]{b}-b\sqrt[]{a}-b\sqrt[]{b}}{a-b} \frac{a\sqrt[]{a}+a\sqrt[]{b}-b\sqrt[]{a}-b\sqrt[]{b}}{a-b}](/latexrender/pictures/d44e9bbebb6c4a01f2288595c3a64731.png)
«
Resultado pelo gabarito :
![\sqrt[]{a}+\sqrt[]{b} \sqrt[]{a}+\sqrt[]{b}](/latexrender/pictures/17957293567ab489803a1248360d8334.png)
![\frac{a - b}{\sqrt[]{a} - \sqrt[]{b}} \frac{a - b}{\sqrt[]{a} - \sqrt[]{b}}](/latexrender/pictures/df556b3fae7f7f752c6a39ae4f95d915.png)
=
![\left(\frac{a - b}{\sqrt[]{a} - \sqrt[]{b}} \right).\left(\frac{\sqrt[]{a} + \sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} \right) \left(\frac{a - b}{\sqrt[]{a} - \sqrt[]{b}} \right).\left(\frac{\sqrt[]{a} + \sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} \right)](/latexrender/pictures/230998b4496f5237a2199d145d7f3094.png)
=
![\frac{(a - b)(\sqrt[]{a} + \sqrt[]{b})}{a - b} \frac{(a - b)(\sqrt[]{a} + \sqrt[]{b})}{a - b}](/latexrender/pictures/c6e6d25414ab901201fd118ffae3f626.png)
=
Até aqui vc fez, não precisava aplicar distributiva no numerador, Simplifique.
![\frac{1(\sqrt[]{a} + \sqrt[]{b})}{1} \frac{1(\sqrt[]{a} + \sqrt[]{b})}{1}](/latexrender/pictures/c04b370d3ac2ecaaf13762c6c55799c0.png)
=
![\sqrt[]{a} + \sqrt[]{b} \sqrt[]{a} + \sqrt[]{b}](/latexrender/pictures/2e9c7b25c2340c81571cc55454c06f8c.png)
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Ter Abr 24, 2012 20:14
por DanielFerreira » Ter Abr 24, 2012 20:14
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida em simplificações de radicais
por LuizCarlos » Qui Mai 03, 2012 21:36
- 1 Respostas
- 760 Exibições
- Última mensagem por DanielFerreira

Qui Mai 03, 2012 21:44
Álgebra Elementar
-
- Radicais
por agfp5 » Sáb Out 30, 2010 08:50
- 2 Respostas
- 2340 Exibições
- Última mensagem por agfp5

Sáb Out 30, 2010 09:10
Geometria Plana
-
- Radicais
por Andrewo » Qua Fev 01, 2012 13:43
- 8 Respostas
- 4132 Exibições
- Última mensagem por LuizAquino

Qua Fev 08, 2012 12:22
Álgebra Elementar
-
- Radicais II
por Andrewo » Qui Fev 09, 2012 19:38
- 3 Respostas
- 1882 Exibições
- Última mensagem por MarceloFantini

Sex Fev 10, 2012 11:32
Álgebra Elementar
-
- Radicais de nv
por Andrewo » Seg Fev 13, 2012 16:58
- 4 Respostas
- 2464 Exibições
- Última mensagem por Arkanus Darondra

Ter Fev 14, 2012 13:01
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[12]{{2}^{3}.{a}^{6}} \sqrt[12]{{2}^{3}.{a}^{6}}](/latexrender/pictures/2132be55b04d27134c15735f3bd39d1f.png)
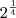 e
e 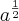
![\sqrt[4]{2} \sqrt[4]{2}](/latexrender/pictures/2f92f26b5ec4b063312e1be4bafd7452.png) e
e ![\sqrt[]{a} \sqrt[]{a}](/latexrender/pictures/3d48e387f88a173a4e4cf3b38dbab4a6.png)
![\sqrt[4]{2.{a}^{2}} \sqrt[4]{2.{a}^{2}}](/latexrender/pictures/ce73b25dcff3d2c7167d63e5e79adcf9.png) ????
????![{(1-\sqrt[]{2})}^{2} {(1-\sqrt[]{2})}^{2}](/latexrender/pictures/064ba63db0deade10f842f254c26b8dc.png)
![(3-\sqrt[]{2}) (3-\sqrt[]{2})](/latexrender/pictures/65e7f9b3a3917d9ea8cd8e3083e426fa.png)
![(3-\sqrt[]{2})(3-\sqrt[]{2}) (3-\sqrt[]{2})(3-\sqrt[]{2})](/latexrender/pictures/58f7576051e80abb42df2fce604d58aa.png) =
=![9-12\sqrt[]{2} + 8 = 17-12\sqrt[]{2} 9-12\sqrt[]{2} + 8 = 17-12\sqrt[]{2}](/latexrender/pictures/280d932b46b0639153364cdd24ff81b8.png)
![\frac{a-b}{\sqrt[]{a}-\sqrt[]{b}} \frac{a-b}{\sqrt[]{a}-\sqrt[]{b}}](/latexrender/pictures/adcfd5a77f7da6b1e6ac10b12505fc59.png) b
b ![\frac{a-b}{\sqrt[]{a}-\sqrt[]{b}}.\frac{\sqrt[]{a}+\sqrt[]{b}}{\sqrt[]{a}+\sqrt[]{b}} \frac{a-b}{\sqrt[]{a}-\sqrt[]{b}}.\frac{\sqrt[]{a}+\sqrt[]{b}}{\sqrt[]{a}+\sqrt[]{b}}](/latexrender/pictures/4a80b60f385b88a718fa9bbdfb1e334e.png)
![\frac{a\sqrt[]{a}+a\sqrt[]{b}-b\sqrt[]{a}-b\sqrt[]{b}}{a-b} \frac{a\sqrt[]{a}+a\sqrt[]{b}-b\sqrt[]{a}-b\sqrt[]{b}}{a-b}](/latexrender/pictures/d44e9bbebb6c4a01f2288595c3a64731.png) «
«![\sqrt[]{a}+\sqrt[]{b} \sqrt[]{a}+\sqrt[]{b}](/latexrender/pictures/17957293567ab489803a1248360d8334.png)





![\sqrt[12]{2^3.a^6} = \sqrt[12]{2^3.a^6} =](/latexrender/pictures/61c755686471832d3ae75f87ff57e5bb.png)
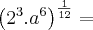
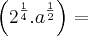
![\sqrt[4]{2} . \sqrt[]{a} = \sqrt[4]{2} . \sqrt[]{a} =](/latexrender/pictures/60049d51c311b108664f5f6a26ca8674.png)
![\sqrt[n]{x} \sqrt[n]{x}](/latexrender/pictures/13fcbed8bcac58d95c0cb989f3aca2de.png)
![\sqrt[4]{2} . \sqrt[4]{a^2} = \sqrt[4]{2} . \sqrt[4]{a^2} =](/latexrender/pictures/fb4f6f82d647fbd97a0dcf9cff77a778.png)
![\sqrt[4]{2.a^2} \sqrt[4]{2.a^2}](/latexrender/pictures/d81727c89e463f38666e8a3633fe55d0.png)

![(1 - \sqrt[]{2})^2(3 - \sqrt[]{2}) = (1 - \sqrt[]{2})^2(3 - \sqrt[]{2}) =](/latexrender/pictures/8077873616e12b369d8ea4e305d67eb8.png)
![(1 - 2\sqrt[]{2} + 2)(3 - \sqrt[]{2}) = (1 - 2\sqrt[]{2} + 2)(3 - \sqrt[]{2}) =](/latexrender/pictures/c67779cec3dba68dbec8b388ecc68b8c.png)
![(3 - 2\sqrt[]{2})(3 - \sqrt[]{2}) = (3 - 2\sqrt[]{2})(3 - \sqrt[]{2}) =](/latexrender/pictures/ffa52ccb838ed4a12b592d69214cce51.png)
![(3 - 2\sqrt[]{2}) \neq(3 - \sqrt[]{2}) (3 - 2\sqrt[]{2}) \neq(3 - \sqrt[]{2})](/latexrender/pictures/25aad3d31e331c1175a7084b93886e4c.png)
![9 - 3\sqrt[]{2} - 6\sqrt[]{2} + 4 = 9 - 3\sqrt[]{2} - 6\sqrt[]{2} + 4 =](/latexrender/pictures/0de36282adb00ba1ef22579cfa05267c.png)
![13 - 9\sqrt[]{2} 13 - 9\sqrt[]{2}](/latexrender/pictures/0a7db61fc6505df805c802fa52f8746d.png)
![\frac{a - b}{\sqrt[]{a} - \sqrt[]{b}} \frac{a - b}{\sqrt[]{a} - \sqrt[]{b}}](/latexrender/pictures/df556b3fae7f7f752c6a39ae4f95d915.png) =
=![\left(\frac{a - b}{\sqrt[]{a} - \sqrt[]{b}} \right).\left(\frac{\sqrt[]{a} + \sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} \right) \left(\frac{a - b}{\sqrt[]{a} - \sqrt[]{b}} \right).\left(\frac{\sqrt[]{a} + \sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} \right)](/latexrender/pictures/230998b4496f5237a2199d145d7f3094.png) =
=![\frac{(a - b)(\sqrt[]{a} + \sqrt[]{b})}{a - b} \frac{(a - b)(\sqrt[]{a} + \sqrt[]{b})}{a - b}](/latexrender/pictures/c6e6d25414ab901201fd118ffae3f626.png) =
=![\frac{1(\sqrt[]{a} + \sqrt[]{b})}{1} \frac{1(\sqrt[]{a} + \sqrt[]{b})}{1}](/latexrender/pictures/c04b370d3ac2ecaaf13762c6c55799c0.png) =
=![\sqrt[]{a} + \sqrt[]{b} \sqrt[]{a} + \sqrt[]{b}](/latexrender/pictures/2e9c7b25c2340c81571cc55454c06f8c.png)

 , avisa que eu resolvo.
, avisa que eu resolvo.

