quase todos os templos gregos. Do ponto de vista da geometria, sua fachada é retangular (ver figura) e possui
medidas especiais, obtidas da seguinte maneira: toma-se um segmento de comprimento l e divide-se em duas
partes, de tal forma que a razão entre o segmento todo (l) e a parte maior (x) seja igual à razão entre a parte maior e a
parte menor. A parte maior seria a base do retângulo, e a menor, a altura. Assinale a alternativa que indica essa
razão.

R:
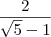
Encontrei uma resolução no wikipédia, porém gostaria de uma explicação para o primeiro passo(...):

(...) e para a contextualização do mesmo para o seguinte trecho do enunciado: "toma-se um segmento de comprimento l e divide-se em duas
partes, de tal forma que a razão entre o segmento todo (l) e a parte maior (x) seja igual à razão entre a parte maior e a
parte menor. A parte maior seria a base do retângulo, e a menor, a altura."
Grato.


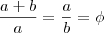
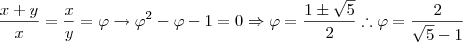
![\varphi = \frac{1+\sqrt[]{5}}{2} \varphi = \frac{1+\sqrt[]{5}}{2}](/latexrender/pictures/b95569b387932542d657922b2b2464b3.png)

 .
.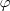 e somar 1 tera a resposta dada pelo problema.
e somar 1 tera a resposta dada pelo problema. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
