 por Arkanus Darondra » Ter Abr 17, 2012 00:38
por Arkanus Darondra » Ter Abr 17, 2012 00:38
O Partenon, construído em Atenas, na Grécia Antiga, exemplifica o estilo e as proporções que se encontram em
quase todos os templos gregos. Do ponto de vista da geometria, sua fachada é retangular (ver figura) e possui
medidas especiais, obtidas da seguinte maneira: toma-se um segmento de comprimento l e divide-se em duas
partes, de tal forma que a razão entre o segmento todo (l) e a parte maior (x) seja igual à razão entre a parte maior e a
parte menor. A parte maior seria a base do retângulo, e a menor, a altura. Assinale a alternativa que indica essa
razão.
 R:
R: 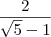
Encontrei uma resolução no wikipédia, porém gostaria de uma explicação para o primeiro passo(...):

(...) e para a contextualização do mesmo para o seguinte trecho do enunciado: "toma-se um segmento de comprimento l e divide-se em duas
partes, de tal forma que a razão entre o segmento todo (l) e a parte maior (x) seja igual à razão entre a parte maior e a
parte menor. A parte maior seria a base do retângulo, e a menor, a altura."
Grato.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Qua Abr 18, 2012 23:46
por fraol » Qua Abr 18, 2012 23:46
Boa noite,
Não estou certo que entendi a sua dúvida, mas como o forum serve para discutir, divergir ou convergir quando possível, vamos lá:
A proporção áurea é uma definição.
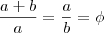
Nessa fórmula está aplicada a definição: a razão entre o todo (a+b) pela parte maior (a) é igual à razão entre a parte maior (a) pela parte menor (b) . Se duas medidas guardarem essa relação então elas estarão em proporção áurea.
Abç.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Arkanus Darondra » Sáb Abr 21, 2012 00:13
por Arkanus Darondra » Sáb Abr 21, 2012 00:13
Boa Noite.
Perdão. Não expressei minha dúvida claramente. Estava tentando apenas relacionar a e b com os dados do enunciado
Acho que consegui:
Chamando o lado menor de y e o maior de x, temos que, pela fórmula acima, a=x e b=y. Então:
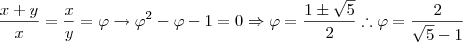
Me corrija se estiver errado.
Outra coisa... Neste caso, como l é dividido ao meio dando origem a x e y, devo considerá-lo como sendo uma espécie de planificação da altura, "juntando" esta com a base em linha reta?
Grato.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Sáb Abr 21, 2012 00:34
por Russman » Sáb Abr 21, 2012 00:34
A razão áurea é comumente escrita como
![\varphi = \frac{1+\sqrt[]{5}}{2} \varphi = \frac{1+\sqrt[]{5}}{2}](/latexrender/pictures/b95569b387932542d657922b2b2464b3.png)
Porém, devido a sua própria definição, existe a identidade

que qualifica

.
Assim, se vc tomar o inverso de
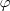
e somar 1 tera a resposta dada pelo problema.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Triangulo retangulo razão aurea
por benni » Sáb Mar 26, 2011 15:08
- 0 Respostas
- 1374 Exibições
- Última mensagem por benni

Sáb Mar 26, 2011 15:08
Geometria Plana
-
- Demonstração da razão aurea no pentagono.
por benni » Dom Out 16, 2011 15:13
- 2 Respostas
- 2435 Exibições
- Última mensagem por benni

Sáb Out 22, 2011 13:14
Geometria Plana
-
- [Áreas: Triângulos retângulos] Razão áurea
 por Gustavo Gomes » Sex Out 19, 2012 22:58
por Gustavo Gomes » Sex Out 19, 2012 22:58
- 1 Respostas
- 1495 Exibições
- Última mensagem por e8group

Sáb Out 20, 2012 01:24
Geometria Plana
-
- Proporção
por Roberta » Ter Jul 14, 2009 17:22
- 2 Respostas
- 3164 Exibições
- Última mensagem por Roberta

Ter Jul 14, 2009 19:53
Desafios Enviados
-
- PROPORÇÃO
por patriciagarciapoa » Qui Nov 05, 2009 16:37
- 1 Respostas
- 1775 Exibições
- Última mensagem por Lucio Carvalho

Qui Nov 05, 2009 17:14
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

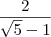



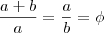
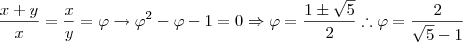
![\varphi = \frac{1+\sqrt[]{5}}{2} \varphi = \frac{1+\sqrt[]{5}}{2}](/latexrender/pictures/b95569b387932542d657922b2b2464b3.png)

 .
.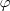 e somar 1 tera a resposta dada pelo problema.
e somar 1 tera a resposta dada pelo problema.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.