 por vmouc » Ter Mar 27, 2012 14:53
por vmouc » Ter Mar 27, 2012 14:53
Pessoal,
Essa questão caiu na minha prova de Calculo, ontem. Por favor me dêem uma ajuda pra entender.
Encontre o cumprimento da curva:
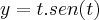
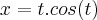
nos limites
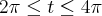
.
Fiz da seguinte forma:
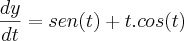
pela regra do produto (derivação)
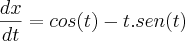
Aplicando na equação de comprimento da curva:
![\int_{}^{}\sqrt[]{\left(\frac{dy}{dt} \right)^2+\left(\frac{dx}{dt} \right)^2 dt} \int_{}^{}\sqrt[]{\left(\frac{dy}{dt} \right)^2+\left(\frac{dx}{dt} \right)^2 dt}](/latexrender/pictures/33cc0036a6033b6fe14d2241a6023406.png)
Onde por regra o resultado seria:
![\int_{}^{}\sqrt[]{a^2+u^2}du= \frac{u}{2}\sqrt[]{a^2+u^2}+\frac{a^2}{2}ln\left|u+\sqrt[]{a^2+u^2} \right|+C \int_{}^{}\sqrt[]{a^2+u^2}du= \frac{u}{2}\sqrt[]{a^2+u^2}+\frac{a^2}{2}ln\left|u+\sqrt[]{a^2+u^2} \right|+C](/latexrender/pictures/387f025849ea579d1d1e26d665e9978a.png)
![\frac{cos(t)-t.sen(t)}{2}.\sqrt[]{\left(sen^2t + t^2.cos^2t \right)+ \left(cos^2t + t^2sen^2t \right)} + \frac{sen^2t + t^2cos^2t}{2} \frac{cos(t)-t.sen(t)}{2}.\sqrt[]{\left(sen^2t + t^2.cos^2t \right)+ \left(cos^2t + t^2sen^2t \right)} + \frac{sen^2t + t^2cos^2t}{2}](/latexrender/pictures/1a1be7513ef0d83039cb78065af8230c.png)
.
![ln\left|\left(cos(t)-tsen(t) \right) +\sqrt[]{\left(sen^2t+t^2cos^2t \right)+\left(cos^2t +t^2sen^2t \right)}\right|+C ln\left|\left(cos(t)-tsen(t) \right) +\sqrt[]{\left(sen^2t+t^2cos^2t \right)+\left(cos^2t +t^2sen^2t \right)}\right|+C](/latexrender/pictures/cbd1afafce59129efed1a9d11c1e8acc.png)
Pra tentar organizar, fiz o seguinte:
OBS:
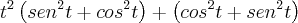
Ficou:
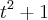
Voltando:
![\frac{cos(t)-tsen(t)}{2}.\sqrt[]{t^2+1^2} + \frac{sen^2(t) + t^2cos^2(t)}{2}ln\left|cos(t)-tsen(t)+\sqrt[]{ t^2+1^2} \right| \frac{cos(t)-tsen(t)}{2}.\sqrt[]{t^2+1^2} + \frac{sen^2(t) + t^2cos^2(t)}{2}ln\left|cos(t)-tsen(t)+\sqrt[]{ t^2+1^2} \right|](/latexrender/pictures/2beace109dd7d611f7eba901669eb66c.png)
Este é o caminho? Ja continuo...
Vinícius Costa
-
vmouc
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Sáb Mar 05, 2011 22:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
-
 por LuizAquino » Ter Mar 27, 2012 18:42
por LuizAquino » Ter Mar 27, 2012 18:42
Aqui você cometeu um erro de interpretação. Note como apenas
decorar "regras" não é uma boa prática.
Nessa "regra" que você exibiu, o termo a² é uma constante. Ou seja, esse termo não depende da variável da integral (que no caso é
u).
Mas quando você aplicou essa "regra", você considerou indevidamente que o termo
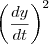
é uma constante. Esse não é o caso, já que esse termo é dependente da variável da integral (que no caso é
t).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por vmouc » Qui Abr 19, 2012 13:59
por vmouc » Qui Abr 19, 2012 13:59
Então não entendo a forma que deveria ser feito. Você poderia só deixar um pouco mais claro de como deveria ser resolvido, por gentileza?
Vinícius Costa
-
vmouc
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Sáb Mar 05, 2011 22:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
-
 por LuizAquino » Qui Abr 19, 2012 15:10
por LuizAquino » Qui Abr 19, 2012 15:10
vmouc escreveu:Então não entendo a forma que deveria ser feito. Você poderia só deixar um pouco mais claro de como deveria ser resolvido, por gentileza?
Você já sabe que:
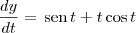
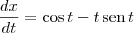
Desse modo, temos que:
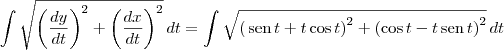
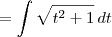
Tente continuar a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações paramétricas da curva
por kalschne » Qui Fev 16, 2012 20:51
- 3 Respostas
- 2124 Exibições
- Última mensagem por kalschne

Qui Fev 16, 2012 22:48
Geometria Analítica
-
- [Equações Paramétricas - Derivada da Curva]
por raimundoocjr » Sáb Out 19, 2013 20:38
- 0 Respostas
- 805 Exibições
- Última mensagem por raimundoocjr

Sáb Out 19, 2013 20:38
Cálculo: Limites, Derivadas e Integrais
-
- [comprimento da curva] Exercicio de comprimento do grafico?
por didone » Sex Abr 12, 2013 17:44
- 1 Respostas
- 1889 Exibições
- Última mensagem por young_jedi

Seg Abr 15, 2013 21:44
Cálculo: Limites, Derivadas e Integrais
-
- Comprimento de curva
por dsbonafe » Ter Out 13, 2009 16:39
- 1 Respostas
- 2761 Exibições
- Última mensagem por Camolas

Sex Mai 31, 2013 15:27
Cálculo: Limites, Derivadas e Integrais
-
- Comprimento da curva
por Crist » Qui Nov 29, 2012 13:32
- 6 Respostas
- 3727 Exibições
- Última mensagem por young_jedi

Ter Dez 11, 2012 11:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
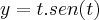
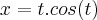
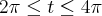 .
.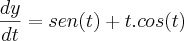 pela regra do produto (derivação)
pela regra do produto (derivação)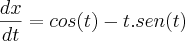
![\int_{}^{}\sqrt[]{\left(\frac{dy}{dt} \right)^2+\left(\frac{dx}{dt} \right)^2 dt} \int_{}^{}\sqrt[]{\left(\frac{dy}{dt} \right)^2+\left(\frac{dx}{dt} \right)^2 dt}](/latexrender/pictures/33cc0036a6033b6fe14d2241a6023406.png)
![\int_{}^{}\sqrt[]{a^2+u^2}du= \frac{u}{2}\sqrt[]{a^2+u^2}+\frac{a^2}{2}ln\left|u+\sqrt[]{a^2+u^2} \right|+C \int_{}^{}\sqrt[]{a^2+u^2}du= \frac{u}{2}\sqrt[]{a^2+u^2}+\frac{a^2}{2}ln\left|u+\sqrt[]{a^2+u^2} \right|+C](/latexrender/pictures/387f025849ea579d1d1e26d665e9978a.png)
![\frac{cos(t)-t.sen(t)}{2}.\sqrt[]{\left(sen^2t + t^2.cos^2t \right)+ \left(cos^2t + t^2sen^2t \right)} + \frac{sen^2t + t^2cos^2t}{2} \frac{cos(t)-t.sen(t)}{2}.\sqrt[]{\left(sen^2t + t^2.cos^2t \right)+ \left(cos^2t + t^2sen^2t \right)} + \frac{sen^2t + t^2cos^2t}{2}](/latexrender/pictures/1a1be7513ef0d83039cb78065af8230c.png) .
. ![ln\left|\left(cos(t)-tsen(t) \right) +\sqrt[]{\left(sen^2t+t^2cos^2t \right)+\left(cos^2t +t^2sen^2t \right)}\right|+C ln\left|\left(cos(t)-tsen(t) \right) +\sqrt[]{\left(sen^2t+t^2cos^2t \right)+\left(cos^2t +t^2sen^2t \right)}\right|+C](/latexrender/pictures/cbd1afafce59129efed1a9d11c1e8acc.png)
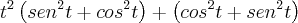
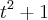
![\frac{cos(t)-tsen(t)}{2}.\sqrt[]{t^2+1^2} + \frac{sen^2(t) + t^2cos^2(t)}{2}ln\left|cos(t)-tsen(t)+\sqrt[]{ t^2+1^2} \right| \frac{cos(t)-tsen(t)}{2}.\sqrt[]{t^2+1^2} + \frac{sen^2(t) + t^2cos^2(t)}{2}ln\left|cos(t)-tsen(t)+\sqrt[]{ t^2+1^2} \right|](/latexrender/pictures/2beace109dd7d611f7eba901669eb66c.png)


![\, . \, ln\left|\left(cos(t)-tsen(t) \right) +\sqrt[]{\left(sen^2t+t^2cos^2t \right)+\left(cos^2t +t^2sen^2t \right)}\right|+C \, . \, ln\left|\left(cos(t)-tsen(t) \right) +\sqrt[]{\left(sen^2t+t^2cos^2t \right)+\left(cos^2t +t^2sen^2t \right)}\right|+C](/latexrender/pictures/48e1160bd21aa4fbbb0aff3110057ade.png)
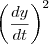 é uma constante. Esse não é o caso, já que esse termo é dependente da variável da integral (que no caso é
é uma constante. Esse não é o caso, já que esse termo é dependente da variável da integral (que no caso é 
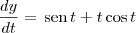
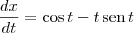
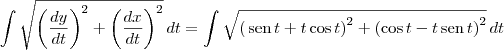
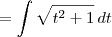
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
