 por jemourafer » Sex Abr 13, 2012 14:51
por jemourafer » Sex Abr 13, 2012 14:51
Como acharia esse intervalos?
" Mostre que a equação
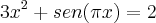
admite duas soluções reais distintas. "
-
jemourafer
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Abr 01, 2012 20:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por MarceloFantini » Sáb Abr 14, 2012 00:17
por MarceloFantini » Sáb Abr 14, 2012 00:17
Precisamos encontrar número tais que a função
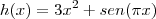
satisfaça
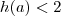
e
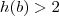
. Vemos que zero parece ser um bom candidato inferior pois
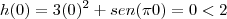
, numa outra tentativa vamos considerar
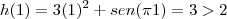
; portanto o intervalo
![[0,1] [0,1]](/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png)
satisfaz os requerimentos. Veja que qualquer intervalo contendo este também satisfará. Trabalhe a partir disso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema do Valor Intermediário
por MCordeiro » Ter Mai 26, 2020 23:00
- 0 Respostas
- 2381 Exibições
- Última mensagem por MCordeiro

Ter Mai 26, 2020 23:00
Cálculo: Limites, Derivadas e Integrais
-
- Duvida no Teorema do valor intermediário.
por TheoFerraz » Sáb Abr 30, 2011 19:32
- 2 Respostas
- 3049 Exibições
- Última mensagem por TheoFerraz

Sáb Abr 30, 2011 19:40
Cálculo: Limites, Derivadas e Integrais
-
- Questão - Polinômio Grau 3 - Teorema do Valor Intermediário
por elisafrombrazil » Sáb Jan 21, 2017 10:41
- 4 Respostas
- 4865 Exibições
- Última mensagem por e8group

Qui Fev 02, 2017 23:41
Cálculo: Limites, Derivadas e Integrais
-
- [Continuidade] Problema de Valor Intermediário
por Imscatman » Seg Out 03, 2011 00:18
- 3 Respostas
- 2344 Exibições
- Última mensagem por Imscatman

Seg Out 03, 2011 02:12
Cálculo: Limites, Derivadas e Integrais
-
- Teomera do valor intermediário - exercício
por Danilo » Sáb Set 14, 2013 14:05
- 0 Respostas
- 1534 Exibições
- Última mensagem por Danilo

Sáb Set 14, 2013 14:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
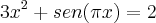 admite duas soluções reais distintas. "
admite duas soluções reais distintas. "
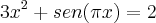 admite duas soluções reais distintas. "
admite duas soluções reais distintas. "
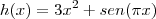 satisfaça
satisfaça 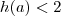 e
e 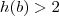 . Vemos que zero parece ser um bom candidato inferior pois
. Vemos que zero parece ser um bom candidato inferior pois 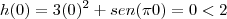 , numa outra tentativa vamos considerar
, numa outra tentativa vamos considerar 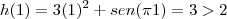 ; portanto o intervalo
; portanto o intervalo ![[0,1] [0,1]](/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) satisfaz os requerimentos. Veja que qualquer intervalo contendo este também satisfará. Trabalhe a partir disso.
satisfaz os requerimentos. Veja que qualquer intervalo contendo este também satisfará. Trabalhe a partir disso.


 .
.
 :
: