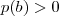por Fabio Wanderley » Sex Abr 13, 2012 23:38
por Fabio Wanderley » Sex Abr 13, 2012 23:38
Olá, colegas
Caiu a seguinte questão na minha prova de Cálculo I:
"Considere o polinômio de grau n, onde n é ímpar, dado por:
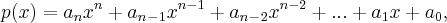
e os
a são todos reais. Mostre, usando a teoria de limites, que p(x) admite pelo menos uma raiz real."
Daí eu respondi exatamente assim:
Toda função polinomial é contínua. E de acordo com o Teorema de Bolzano, em um intervalo [a,b] se f(a) e f(b) tiverem sinais contrários, então haverá pelo menos um c em que f(c) = 0.Pela correção do professor, ele circulou o "f(a)" e o "f(b)" e escreveu "
Isso ocorre no polinômio dado?" E a questão foi zerada.
Minha dúvida então é se eu errei por colocar
f em vez de
p, ou se ela é resolvida corretamente de outra forma.
Desde já agradeço!
-
Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por MarceloFantini » Sáb Abr 14, 2012 00:05
por MarceloFantini » Sáb Abr 14, 2012 00:05
Não foi pela mera troca de nome da função que você errou, mas sim porque simplesmente não resolveu. Seu raciocínio não está errado, porém pense: você exibiu dois pontos tais que um tenha imagem positiva e outro imagem negativa? A resposta é
não.
Como o polinômio tem grau ímpar, temos
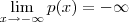
enquanto
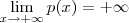
, logo existem pontos
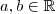
tais que
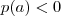
e
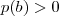 pelo fato que todo polinômio é contínuo
pelo fato que todo polinômio é contínuo. Pelo teorema de Bolzano, segue a conclusão.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Fabio Wanderley » Sáb Abr 14, 2012 00:43
por Fabio Wanderley » Sáb Abr 14, 2012 00:43
Obrigado, Marcelo!
Agora pude ver que realmente não respondi a questão, faltaram os pontos... E eu ainda não havia considerado o "Mostre, usando a teoria de limites(...)"
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Confusão em teoria dos conjuntos numa questão.
 por Debora Bruna » Seg Jan 11, 2016 17:44
por Debora Bruna » Seg Jan 11, 2016 17:44
- 1 Respostas
- 8842 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 23, 2016 16:44
Conjuntos
-
- [PA] Uma dúvida numa questão de PA
por rochadapesada » Qui Abr 04, 2013 22:08
- 3 Respostas
- 2643 Exibições
- Última mensagem por DanielFerreira

Dom Abr 07, 2013 20:28
Progressões
-
- [conjunto] dúvida numa questão da cespe
por Fabio Wanderley » Dom Abr 29, 2012 16:53
- 3 Respostas
- 2424 Exibições
- Última mensagem por MarceloFantini

Seg Mai 28, 2012 22:49
Conjuntos
-
- Questão prova concurso (dúvida)
por fernandocez » Seg Mar 14, 2011 21:35
- 5 Respostas
- 2687 Exibições
- Última mensagem por fernandocez

Qua Mar 16, 2011 00:16
Logaritmos
-
- Questão prova concurso (dúvida na resposta)
 por fernandocez » Qua Mar 16, 2011 13:47
por fernandocez » Qua Mar 16, 2011 13:47
- 3 Respostas
- 2965 Exibições
- Última mensagem por fernandocez

Qua Mar 16, 2011 23:36
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
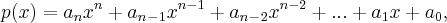


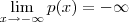 enquanto
enquanto 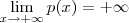 , logo existem pontos
, logo existem pontos 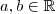 tais que
tais que 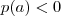 e
e