 por MERLAYNE » Qui Mar 29, 2012 01:46
por MERLAYNE » Qui Mar 29, 2012 01:46
A EXPRESSÃO sen (7pi/6)+sen ( x+11)*cotg (x +11pi/2) /cos (9pi - x), com xE[0,pi/4], é equivalente a:
-
MERLAYNE
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Mar 28, 2012 19:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qui Mar 29, 2012 10:43
por MarceloFantini » Qui Mar 29, 2012 10:43
Merlayne, sua expressão está difícil de ler. Por favor, leia as
regras do fórum, em especial a regra número 2.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MERLAYNE » Ter Abr 03, 2012 09:20
por MERLAYNE » Ter Abr 03, 2012 09:20
MarceloFantini escreveu:Merlayne, sua expressão está difícil de ler. Por favor, leia as
regras do fórum, em especial a regra número 2.
ok ai está reescrita:
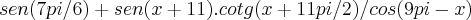
, com xE[0,?/4], é equivalente a:
Editado pela última vez por
MERLAYNE em Qua Abr 04, 2012 19:04, em um total de 1 vez.
-
MERLAYNE
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Mar 28, 2012 19:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Ter Abr 03, 2012 14:57
por MarceloFantini » Ter Abr 03, 2012 14:57
Merlayne, você não leu as regras. Sua expressão não está em LaTeX e você não postou suas tentativas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MERLAYNE » Qua Abr 04, 2012 19:06
por MERLAYNE » Qua Abr 04, 2012 19:06
MarceloFantini escreveu:Merlayne, você não leu as regras. Sua expressão não está em LaTeX e você não postou suas tentativas.
Não postei tentativas pois, não sei fazer! Se soubesse não estaria aqui tirando dúvidas. Obrigada pela correção em relação ao LaTeX.
-
MERLAYNE
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Mar 28, 2012 19:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Abr 04, 2012 19:16
por MarceloFantini » Qua Abr 04, 2012 19:16
Não perguntar se você sabia fazer, perguntou o que você tentou fazer, se tentou manipular as funções, se sabe o que é uma soma de arcos, etc. A expressão correta em LaTeX é
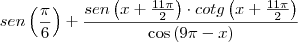
com
![x \in \left[0,\frac{\pi}{4} \right] x \in \left[0,\frac{\pi}{4} \right]](/latexrender/pictures/029d551bcc3533b71f1b08ac7f1935d4.png)
.
As dicas são: lembre-se que
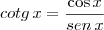
e
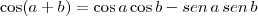
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Redução de quadrante
por Edla Matias » Dom Dez 18, 2011 12:59
- 0 Respostas
- 893 Exibições
- Última mensagem por Edla Matias

Dom Dez 18, 2011 12:59
Trigonometria
-
- redução ao primeiro quadrante
por zenildo » Seg Jun 24, 2013 12:52
- 1 Respostas
- 1697 Exibições
- Última mensagem por Rafael16

Seg Jun 24, 2013 15:53
Trigonometria
-
- redução ao primeiro quadrante
por zenildo » Seg Jun 24, 2013 13:08
- 1 Respostas
- 2688 Exibições
- Última mensagem por Rafael16

Seg Jun 24, 2013 15:41
Trigonometria
-
- redução ao primeiro quadrante
por zenildo » Seg Jun 24, 2013 20:02
- 1 Respostas
- 1308 Exibições
- Última mensagem por zenildo

Qua Jun 26, 2013 20:41
Trigonometria
-
- redução ao primeiro quadrante
por zenildo » Sex Jun 28, 2013 17:38
- 1 Respostas
- 1587 Exibições
- Última mensagem por DanielFerreira

Sáb Jun 29, 2013 09:29
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





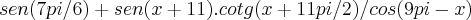 , com xE[0,?/4], é equivalente a:
, com xE[0,?/4], é equivalente a:



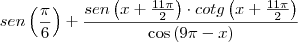 com
com ![x \in \left[0,\frac{\pi}{4} \right] x \in \left[0,\frac{\pi}{4} \right]](/latexrender/pictures/029d551bcc3533b71f1b08ac7f1935d4.png) .
.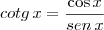 e
e 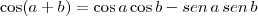 .
.
