 por dileivas » Seg Abr 02, 2012 14:20
por dileivas » Seg Abr 02, 2012 14:20
Oi gente!
Tô com uma dúvida cruel aqui. Na equação diferencial de Bernoulli, para linearizá-la tenho que fazer uma substituição do tipo:
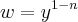
Porém, preciso derivar para concluir a linearização. Na minha cabeça, a derivada disso é:
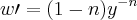
Mas a resposta ainda tem um
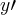
sendo multiplicado, ou seja

Alguém poderia me explicar de onde vem esse
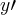
?
Obrigado =)
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
 por MarceloFantini » Seg Abr 02, 2012 19:10
por MarceloFantini » Seg Abr 02, 2012 19:10
Você provavelmente tem algo como
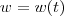
e
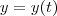
, ou seja, você tem duas funções que dependem de um outro parâmetro

, sendo que a segunda você tem uma composição de

com

. Usando a regra da cadeia, você tem que
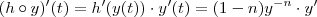
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por dileivas » Seg Abr 02, 2012 19:14
por dileivas » Seg Abr 02, 2012 19:14
Super Obrigado! Preciso estudar melhor essa regra da cadeia! hahaha
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- MAT430 - Seminário: A Família Bernoulli
 por admin » Sex Mai 22, 2009 19:07
por admin » Sex Mai 22, 2009 19:07
- 2 Respostas
- 3467 Exibições
- Última mensagem por admin

Sáb Mai 23, 2009 06:12
História da Matemática
-
- [Ajuda/urgente] equações de Bernoulli
por LBT » Seg Out 18, 2010 16:53
- 0 Respostas
- 1089 Exibições
- Última mensagem por LBT

Seg Out 18, 2010 16:53
Cálculo: Limites, Derivadas e Integrais
-
- [Região de Bernoulli] Calcular a area
por Gustavo182 » Qui Abr 18, 2013 18:54
- 1 Respostas
- 1167 Exibições
- Última mensagem por young_jedi

Sex Abr 19, 2013 21:29
Cálculo: Limites, Derivadas e Integrais
-
- Problema com Derivada
por veldri » Qua Jun 02, 2010 13:51
- 0 Respostas
- 1066 Exibições
- Última mensagem por veldri

Qua Jun 02, 2010 13:51
Cálculo: Limites, Derivadas e Integrais
-
- Problema derivada
 por Herrero088 » Seg Jul 12, 2010 23:31
por Herrero088 » Seg Jul 12, 2010 23:31
- 2 Respostas
- 2715 Exibições
- Última mensagem por Douglasm

Ter Jul 13, 2010 19:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
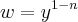
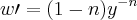
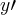 sendo multiplicado, ou seja
sendo multiplicado, ou seja
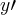 ?
?

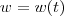 e
e 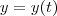 , ou seja, você tem duas funções que dependem de um outro parâmetro
, ou seja, você tem duas funções que dependem de um outro parâmetro  , sendo que a segunda você tem uma composição de
, sendo que a segunda você tem uma composição de  com
com  . Usando a regra da cadeia, você tem que
. Usando a regra da cadeia, você tem que 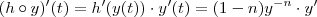 .
.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
