Área do triângulo

[Pri Ferreira]

Considere-se um triângulo escaleno PQR onde M e N
representam, respectivamente, os pontos médios dos
lados PQ e QR. Se a área do quadrilátero PMNR é igual
a 51 m2, a área do triângulo PQR, em m2, é igual a:
(A) 68
(B) 54
(C) 72
(D) 84

Questão de concurso!!!

[LuizAquino]

Considere-se um triângulo escaleno PQR onde M e N
representam, respectivamente, os pontos médios dos
lados PQ e QR. Se a área do quadrilátero PMNR é igual
a 51 m2, a área do triângulo PQR, em m2, é igual a:
(A) 68
(B) 54
(C) 72
(D) 84

A figura abaixo ilustra o exercício.

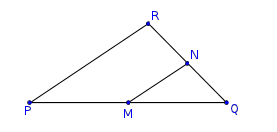
figura.png (9.62 KiB) Exibido 1437 vezes

Como M e N são pontos médios de PQ e QR, pelo Teorema da Base Média, temos que PR é paralelo a MN, sendo que PR = 2*MN.

Note que os triângulos PQR e MQN são semelhantes, sendo que
PR = 2*MN
PQ = 2*MQ
QR = 2*QN

Ou seja, a razão de semelhança entre PQR e MQN é 2. Isso significa que a área de PQR é 4 vezes a área de MQN.

Por fim, temos que a área de PQR é igual a soma entre as áreas de PMNR e MQN.

Agora tente terminar o exercício.