 por Kabection » Sex Mar 23, 2012 23:04
por Kabection » Sex Mar 23, 2012 23:04
Estou confuso na resolução desse limite, o resultado que encontrei foi 1 mas ao usar o software Geogebra o limite dá como resposta 0.5.
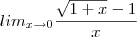
Minha resolução:
1- Multiplico em cima e em baixo por

e fica
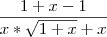
2- Corta 1 com -1 e x em cima com x em baixo resultando em
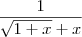
3 - Substituindo o 0 nos x's, fica
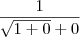
=

=

Alguém poderia me ajudar?
-
Kabection
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jan 16, 2012 15:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por LuizAquino » Sex Mar 23, 2012 23:11
por LuizAquino » Sex Mar 23, 2012 23:11
Kabection escreveu:Estou confuso na resolução desse limite, o resultado que encontrei foi 1 mas ao usar o software Geogebra o limite dá como resposta 0.5.
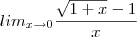
Kabection escreveu:Minha resolução:
1- Multiplico em cima e em baixo por

e fica
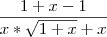
Errado. Ao efetuar essa operação obtemos que:
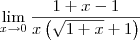
Note que o seu denominador está errado.
Agora continue a resolução considerando essa correção.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Kabection » Sex Mar 23, 2012 23:20
por Kabection » Sex Mar 23, 2012 23:20
Ahh, nossa que besteira eu errei, estava fazendo a distributiva direto. Muito obrigado LCMAquino.
Completando a resolução:
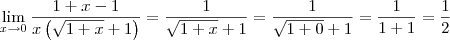
-
Kabection
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jan 16, 2012 15:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por LuizAquino » Sáb Mar 24, 2012 02:36
por LuizAquino » Sáb Mar 24, 2012 02:36
Kabection escreveu:Completando a resolução:
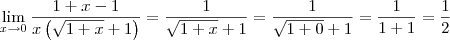
A ideia básica é essa. Mas tome cuidado com a sua escrita. O correto seria:
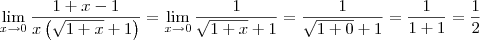
Note que devemos escrever a notação "lim" até antes do momento de aproximar x por 0.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Confusão com pi em derivadas
por Kabection » Seg Abr 16, 2012 23:40
- 1 Respostas
- 906 Exibições
- Última mensagem por emsbp

Ter Abr 17, 2012 13:18
Cálculo: Limites, Derivadas e Integrais
-
- [Conjuntos] Confusão em teoria dos conjuntos numa questão.
 por Debora Bruna » Seg Jan 11, 2016 17:44
por Debora Bruna » Seg Jan 11, 2016 17:44
- 1 Respostas
- 8842 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 23, 2016 16:44
Conjuntos
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6650 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4793 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5126 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
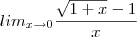
 e fica
e fica 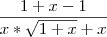
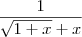
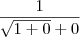 =
=  =
= 

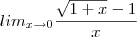
 e fica
e fica 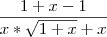
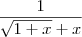
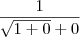 =
=  =
= 

e fica
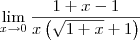

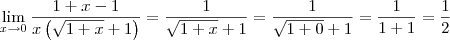

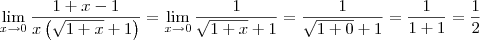


 .
.



