 por lieberth » Seg Jun 15, 2009 19:01
por lieberth » Seg Jun 15, 2009 19:01
boa noite pessoal... (por favor me ajudem) ...
todos os exercícios que faço não estão certos de acordo com meu livro!
estou com duvida nos sinais
ex:
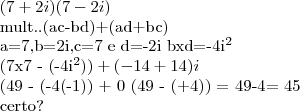
no livro a resposta é 53!
obs..: se eu desconsiderar o sinal da formula a resposta fica correta,ou estou colocando um sinal negativo a mais?
-
lieberth
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Jun 09, 2009 14:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Marcampucio » Seg Jun 15, 2009 19:40
por Marcampucio » Seg Jun 15, 2009 19:40
lieberth escreveu:boa noite pessoal... (por favor me ajudem) ...
todos os exercícios que faço não estão certos de acordo com meu livro!
estou com duvida nos sinais
ex:
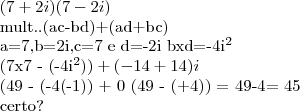
no livro a resposta é 53!
obs..: se eu desconsiderar o sinal da formula a resposta fica correta,ou estou colocando um sinal negativo a mais?
porque você simplesmente não aplica a propriedade distributiva da multipicação?
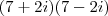
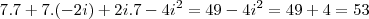
além do mais você poderia notar que esse é um produto notável do tipo
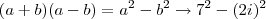
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por lieberth » Ter Jun 16, 2009 15:10
por lieberth » Ter Jun 16, 2009 15:10
OK...
OBRIGADO!
E DESCULPA PELA DOR DE CABEÇA!!!!

-
lieberth
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Jun 09, 2009 14:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Marcampucio » Ter Jun 16, 2009 15:14
por Marcampucio » Ter Jun 16, 2009 15:14
Não há porque se desculpar. Este é o propósito do fórum. O importante é tirar as dúvidas.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17117 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- Numeros complexos!
por Estela » Seg Mar 17, 2008 00:57
- 7 Respostas
- 13360 Exibições
- Última mensagem por andegledson

Seg Nov 02, 2009 21:41
Números Complexos
-
- Números Complexos
por michelle » Dom Ago 31, 2008 15:35
- 3 Respostas
- 10335 Exibições
- Última mensagem por admin

Dom Ago 31, 2008 21:00
Números Complexos
-
- Números Complexos
por Cleyson007 » Qui Mai 14, 2009 13:57
- 7 Respostas
- 13961 Exibições
- Última mensagem por Cleyson007

Sáb Mai 16, 2009 11:04
Números Complexos
-
- NUMEROS COMPLEXOS
por lieberth » Sáb Jun 13, 2009 13:48
- 1 Respostas
- 4111 Exibições
- Última mensagem por Marcampucio

Sáb Jun 13, 2009 14:35
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
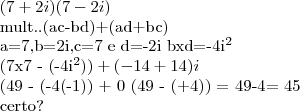

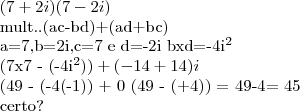

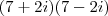
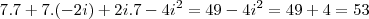
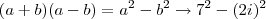




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.