 por MirroR » Dom Mar 18, 2012 18:16
por MirroR » Dom Mar 18, 2012 18:16
Boa tarde. Eu estou cursando o primeiro período do curso de Engenharia, estou utilizando o livro "Um curso de Cálculo, volume 1" pelo Hamilton Luiz Guidorizzi para estudar Cálculo 1.
Nos meus estudos, eu encontrei um problema que não consigo desenvolver
Dado uma função [f(x)=1 + 1/x] precisa-se provar que ela é contínua em p=1.
Eu já tentei várias vezes utilizar da definição elementar de continuidade |f(x)-f(p)|<


|x-p|<

para provar que a função é contínua em p=1, mas no decorrer eu não consigo associar o

ao

. Inclusive, já estou mais avançado no assunto e por outros métodos eu conseguiria provar que a função é contínua, porém é requerido o uso da definição de continuidade.
Por gentileza, ajudem-me a chegar à um resultado.
-
MirroR
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mar 18, 2012 18:00
- Localização: Recife
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Dom Mar 18, 2012 21:38
por LuizAquino » Dom Mar 18, 2012 21:38
MirroR escreveu:Dado uma função [f(x)=1 + 1/x] precisa-se provar que ela é contínua em p=1.
Eu já tentei várias vezes utilizar da definição elementar de continuidade |f(x)-f(p)|<


|x-p|<

para provar que a função é contínua em p=1, mas no decorrer eu não consigo associar o

ao

. Inclusive, já estou mais avançado no assunto e por outros métodos eu conseguiria provar que a função é contínua, porém é requerido o uso da definição de continuidade.
Se f é contínua em x = p, então lembre-se que você precisa provar que:
Para todo

dado, existe
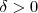
tal que:

Note que você escreveu ao contrário:
MirroR escreveu:
Vejamos agora o desenvolvimento. Note que:







Precisamos agora determinar uma constante
c tal que

.
Como
x está próximo de 1, é razoável dizer que

. Ou seja, temos que

. Note que com isso já estamos escolhendo um valor
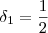
.
Além disso, também podemos dizer que
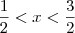
. Ou seja, temos

. Desse modo, temos que:

Note que se fizermos

(o que significa que estamos escolhendo um

), temos que:


Como temos dois valores para delta (
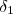
e

), devemos tomar o menor deles para garantir que ao mesmo tempo ocorra as duas inequações:

e

.
Isto é, vamos tomar

.
Agora vamos verificar que essa escolha de

funciona.
Se

, então temos que:

Já havíamos determinado que

. Sendo assim, podemos dizer que:

Multiplicando membro a membro as duas inequações que aparecem depois da implicação, temos que:







-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Continuidade - Dúvida questão, é urgente!!
por arthurvct » Seg Mai 06, 2013 18:37
- 1 Respostas
- 1105 Exibições
- Última mensagem por e8group

Seg Mai 06, 2013 22:11
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade
por AlbertoAM » Seg Abr 04, 2011 20:59
- 8 Respostas
- 5685 Exibições
- Última mensagem por LuizAquino

Qua Abr 06, 2011 10:33
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade
por guilherme5088 » Sáb Out 12, 2019 15:31
- 1 Respostas
- 5333 Exibições
- Última mensagem por adauto martins

Ter Out 15, 2019 23:11
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade
por MCordeiro » Qui Jul 16, 2020 19:11
- 1 Respostas
- 3540 Exibições
- Última mensagem por adauto martins

Qua Out 14, 2020 12:00
Cálculo: Limites, Derivadas e Integrais
-
- Exercicio de Continuidade
por PeIdInHu » Qua Jul 14, 2010 21:04
- 2 Respostas
- 3064 Exibições
- Última mensagem por PeIdInHu

Qui Jul 15, 2010 01:03
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 |x-p|<
|x-p|<  para provar que a função é contínua em p=1, mas no decorrer eu não consigo associar o
para provar que a função é contínua em p=1, mas no decorrer eu não consigo associar o  ao
ao  . Inclusive, já estou mais avançado no assunto e por outros métodos eu conseguiria provar que a função é contínua, porém é requerido o uso da definição de continuidade.
. Inclusive, já estou mais avançado no assunto e por outros métodos eu conseguiria provar que a função é contínua, porém é requerido o uso da definição de continuidade.

 dado, existe
dado, existe 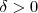 tal que:
tal que:








 .
. . Ou seja, temos que
. Ou seja, temos que  . Note que com isso já estamos escolhendo um valor
. Note que com isso já estamos escolhendo um valor 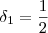 .
.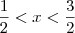 . Ou seja, temos
. Ou seja, temos  . Desse modo, temos que:
. Desse modo, temos que:
 (o que significa que estamos escolhendo um
(o que significa que estamos escolhendo um  ), temos que:
), temos que:
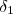 e
e  ), devemos tomar o menor deles para garantir que ao mesmo tempo ocorra as duas inequações:
), devemos tomar o menor deles para garantir que ao mesmo tempo ocorra as duas inequações:  e
e  .
.
 . Sendo assim, podemos dizer que:
. Sendo assim, podemos dizer que:










 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.