dina ribeiro escreveu:Mas u=-5s ou u=s ??????
Se fosse igual a s , ficaria assim:
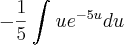
Não entendi!
dina ribeiro escreveu:simmmm, então pq ele disse que tenho que substituir o s por u, se u=-5s????
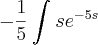
Se u=-5s, então
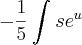
Onde está o erro????
Você interpretou errado o que eu disse.
Eu não disse que você deveria fazer s = u.
O que eu disse foi: "
Note que na sua resolução, a variável s continuou aparecendo na integral após a substituição. Isso não pode acontecer. Afinal de contas, você desejava substituir a variável da integral que era s por uma outra variável (no caso u)".
No método da substituição, nós devemos "substituir" ou "trocar" a variável original da integral por uma outra variável.
Vamos supor que a variável original da integral fosse s. Dizer que vamos "substituir" (ou "trocar") a variável original da integral por u, não significa dizer que vamos fazer s = u. Significa apenas que a integral passará da forma
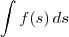
para a forma
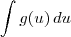
.
Voltando ao exercício, a integral estava no formato:
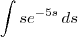
Nesse caso, podemos dizer que
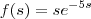
e que portanto a integral tem o formato:
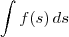
Desejamos agora fazer uma substituição (uma troca) de variável de modo que o novo formato será:
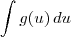
Fazendo então u = -5s (o que é o mesmo que dizer que s = -u/5), temos que a integral original será reescrita como:
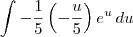
Nesse caso, temos que
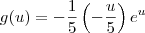
.
O seu erro está no fato de que após a sua substituição o integrando continuou dependendo da variável s. Isto é, não temos apenas uma função do tipo g(u).
Eis o que você escreveu:
dina ribeiro escreveu: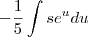
Note que no integrando a variável s continuou aparecendo. Isso não pode acontecer quando usamos a técnica de substituição.
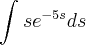
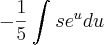
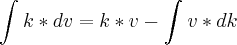
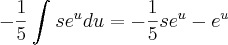
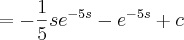

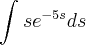
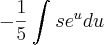
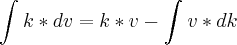
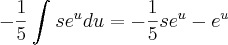
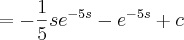

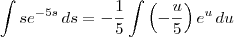

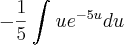


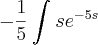
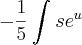



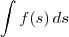 para a forma
para a forma 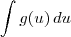 .
.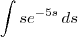
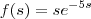 e que portanto a integral tem o formato:
e que portanto a integral tem o formato: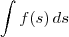
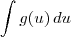
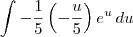
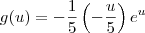 .
.

