
sei que o resultado é
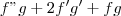 e a questão pede para provar derivando até a segunda ordem que uma é igual a outra.
e a questão pede para provar derivando até a segunda ordem que uma é igual a outra.já entendo como derivar com numeros mas não consegui associar com este tipo de função.
Agradeço desde já.


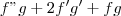 e a questão pede para provar derivando até a segunda ordem que uma é igual a outra.
e a questão pede para provar derivando até a segunda ordem que uma é igual a outra.
miumatos escreveu:Bom dia pessoal, preciso de uma ajuda para entender a seguinte função:
sei que o resultado ée a questão pede para provar derivando até a segunda ordem que uma é igual a outra.
já entendo como derivar com numeros mas não consegui associar com este tipo de função.
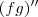 .
.![[(fg)^{\prime}]^{\prime} [(fg)^{\prime}]^{\prime}](/latexrender/pictures/350db2a3bf8316181307de0b5b15aa20.png) .
.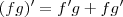
![(fg)^{\prime\prime} = [(fg)^{\prime}]^{\prime} (fg)^{\prime\prime} = [(fg)^{\prime}]^{\prime}](/latexrender/pictures/04d487b63e678689dcf7b1c6f1f7d4af.png)
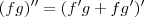
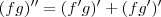
![(fg)^{\prime\prime} = [(f^\prime)^\prime g + f^\prime g^\prime] + [f^\prime g^\prime + f (g^\prime)^\prime] (fg)^{\prime\prime} = [(f^\prime)^\prime g + f^\prime g^\prime] + [f^\prime g^\prime + f (g^\prime)^\prime]](/latexrender/pictures/100a0dd9f5de7213d4259287b4eedda0.png)




Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes

 .
.
 :
: