 por dina ribeiro » Qui Mar 15, 2012 21:20
por dina ribeiro » Qui Mar 15, 2012 21:20
Boa noite!
Gostaria de entender como foi resolvida essa integral . (Essa resolução é do livro)
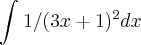
=
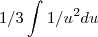
com [u=3x+1 , du=3 dx]
Não consigo enxergar a constante 1/3 que saiu da integral
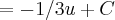
![=-1/[3*(3x+1)] + C =-1/[3*(3x+1)] + C](/latexrender/pictures/6ca0a9ce4e3a3f4945adce93c839d4cf.png)
Grata
-
dina ribeiro
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Mar 15, 2012 19:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por fraol » Qui Mar 15, 2012 21:31
por fraol » Qui Mar 15, 2012 21:31
Veja que você pode escrever
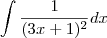
da seguinte forma:
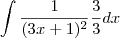
, pois
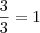
. Então podemos prosseguir assim:
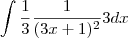
e, por fim, assim:
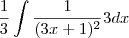
Agora é aplicar a substituição sugerida pelo livro.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por dina ribeiro » Qui Mar 15, 2012 21:53
por dina ribeiro » Qui Mar 15, 2012 21:53
fraol escreveu:Veja que você pode escrever
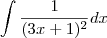
da seguinte forma:
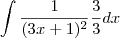
, pois
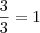
. Então podemos prosseguir assim:
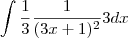
e, por fim, assim:
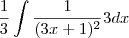
Agora é aplicar a substituição sugerida pelo livro.
Obrigada!!!
-
dina ribeiro
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Mar 15, 2012 19:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por dina ribeiro » Qui Mar 15, 2012 22:25
por dina ribeiro » Qui Mar 15, 2012 22:25
Gostaria de entender essa regra: u = 3x+1
Em uma das tentativas em resolver a integral usei :
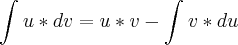
sendo
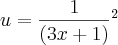
e dv= dx
E em outra tentativa simplemente a integral deu ln (3x+1)².
E possível que me explique passo a passo como foi feito a respota do livro.
Grata
-
dina ribeiro
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Mar 15, 2012 19:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por fraol » Qui Mar 15, 2012 23:24
por fraol » Qui Mar 15, 2012 23:24
fraol escreveu:Veja que você pode escrever
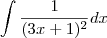
da seguinte forma:
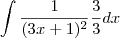
, pois
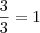
. Então podemos prosseguir assim:
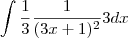
e, por fim, assim:
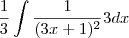
Agora é aplicar a substituição sugerida pelo livro.
Assim vamos continuar:
Se você fizer a substituição sugerida:
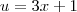
então derivando essa expressão em relação a x você tem:
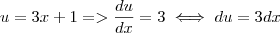
.
Voltando na integral que desenvolvemos e fazendo a substituição:
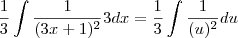
Agora é o momento de desenvolver a integral de

que é igual a
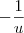
.
Assim
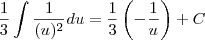
.
Agora é desfazer a substituição de u e você terá a expressão do livro.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Re: Resolução para este problema com explicação:
por drikapic » Sex Out 04, 2013 18:21
- 1 Respostas
- 1086 Exibições
- Última mensagem por Russman

Sáb Out 05, 2013 01:33
Matemática Financeira
-
- Integral - Resolução de integral indefinida.
por brunoisoppo » Qui Mar 03, 2016 15:26
- 0 Respostas
- 3452 Exibições
- Última mensagem por brunoisoppo

Qui Mar 03, 2016 15:26
Cálculo: Limites, Derivadas e Integrais
-
- Resolução de Integral
por suziquim » Qua Jun 08, 2011 13:18
- 4 Respostas
- 2566 Exibições
- Última mensagem por suziquim

Qui Jun 09, 2011 12:04
Cálculo: Limites, Derivadas e Integrais
-
- Resolução de Integral -
por vmouc » Dom Ago 21, 2011 15:01
- 2 Respostas
- 1823 Exibições
- Última mensagem por Neperiano

Dom Ago 21, 2011 15:25
Cálculo: Limites, Derivadas e Integrais
-
- [Resolução de integral]
por adomingues » Sex Jan 20, 2012 16:45
- 2 Respostas
- 1818 Exibições
- Última mensagem por ant_dii

Sáb Jan 21, 2012 02:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
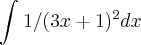
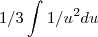
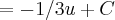
![=-1/[3*(3x+1)] + C =-1/[3*(3x+1)] + C](/latexrender/pictures/6ca0a9ce4e3a3f4945adce93c839d4cf.png)

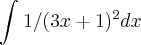
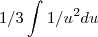
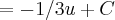
![=-1/[3*(3x+1)] + C =-1/[3*(3x+1)] + C](/latexrender/pictures/6ca0a9ce4e3a3f4945adce93c839d4cf.png)

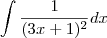 da seguinte forma:
da seguinte forma: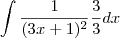 , pois
, pois 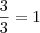 . Então podemos prosseguir assim:
. Então podemos prosseguir assim: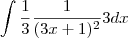 e, por fim, assim:
e, por fim, assim: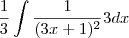

da seguinte forma:
, pois
. Então podemos prosseguir assim:
e, por fim, assim:

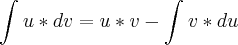
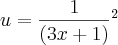 e dv= dx
e dv= dx
da seguinte forma:
, pois
. Então podemos prosseguir assim:
e, por fim, assim:
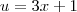 então derivando essa expressão em relação a x você tem:
então derivando essa expressão em relação a x você tem: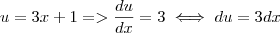 .
.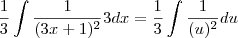
 que é igual a
que é igual a 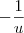 .
.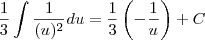 .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

