 por dileivas » Qua Mar 14, 2012 21:32
por dileivas » Qua Mar 14, 2012 21:32
Sinceramente, não entendi o enunciado do exercício, se alguém puder me dar uma luz de como iniciá-lo eu agradeceria muito:
É possível garantir a unicidade de solução para a equação diferencial
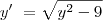
passando pelo ponto (1,4)? E passando pelo ponto (2, -3)? Justifique.
Obrigado! =)
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
 por TheoFerraz » Qua Mar 14, 2012 22:51
por TheoFerraz » Qua Mar 14, 2012 22:51
dileivas escreveu:Sinceramente, não entendi o enunciado do exercício, se alguém puder me dar uma luz de como iniciá-lo eu agradeceria muito:
É possível garantir a unicidade de solução para a equação diferencial
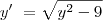
passando pelo ponto (1,4)? E passando pelo ponto (2, -3)? Justifique.
Obrigado! =)
É até que simples. é possível resolver a questão sem resolver a equação até... Sempre que o exercicio pedir para "garantir a unicidade" ele quer que voce prove que só existe uma resposta (ou não). No caso ele quer que voce simplesmente verifique: "existe uma só resposta? ou não"
se voce está estudando "introdução às edo's " eu imagino que esse exercicio é teórico mesmo, não é para ser provado resolvendo a equação.
Voce conhece a ideia de "condições de contorno" ? Se sim, deve ser facil responder a pergunta:
Existe só UMA função que passa por (1,4) e resolve a equação diferencial ordinária
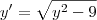
quer uma dica? outra forma de escrever a mesma equação é:

-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por dileivas » Qui Mar 15, 2012 00:07
por dileivas » Qui Mar 15, 2012 00:07
Super obrigado, vou tentar resolver e já posto minha solução =D
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Livro EDO: Introdução às Equações Diferenciais Ordinárias
 por admin » Sáb Jul 21, 2007 19:59
por admin » Sáb Jul 21, 2007 19:59
- 2 Respostas
- 6102 Exibições
- Última mensagem por bruno_dias

Ter Set 01, 2009 01:54
Cálculo
-
- [EQUAÇÕES DIFERENCIAIS ORDINÁRIAS]
por NavegantePI » Qui Mar 02, 2017 00:43
- 0 Respostas
- 6292 Exibições
- Última mensagem por NavegantePI

Qui Mar 02, 2017 00:43
Equações
-
- [Equações Diferenciais Ordinárias e Aplicações]Duvidas
por pdss » Qua Dez 07, 2011 17:56
- 1 Respostas
- 2011 Exibições
- Última mensagem por LuizAquino

Qua Dez 07, 2011 20:14
Cálculo: Limites, Derivadas e Integrais
-
- [PROBLEMAS DE MODELAGEM] EQUAÇÕES DIFERENCIAIS ORDINÁRIAS
 por DanielGL » Ter Mai 03, 2016 14:55
por DanielGL » Ter Mai 03, 2016 14:55
- 1 Respostas
- 3254 Exibições
- Última mensagem por adauto martins

Sex Mai 06, 2016 19:12
Cálculo: Limites, Derivadas e Integrais
-
- Equações Diferencias Ordinárias- Urgente
 por leroaquino » Sáb Set 19, 2015 14:17
por leroaquino » Sáb Set 19, 2015 14:17
- 0 Respostas
- 1376 Exibições
- Última mensagem por leroaquino

Sáb Set 19, 2015 14:17
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
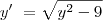 passando pelo ponto (1,4)? E passando pelo ponto (2, -3)? Justifique.
passando pelo ponto (1,4)? E passando pelo ponto (2, -3)? Justifique.
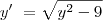 passando pelo ponto (1,4)? E passando pelo ponto (2, -3)? Justifique.
passando pelo ponto (1,4)? E passando pelo ponto (2, -3)? Justifique.
passando pelo ponto (1,4)? E passando pelo ponto (2, -3)? Justifique.



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
