Seja f a função que associa, a cada número real x, o menor dos números x + 3 e - x + 5. Assim, o valor máximo de f(x) é: gaba 4
Não faço ideia de como interpretar esse enunciado logo nem sei como fazê-lo.
Grato
por ViniRFB » Ter Mar 06, 2012 19:57
por fraol » Ter Mar 06, 2012 20:43
é uma função crescente e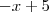 
é uma função descrescente ( em particular são duas retas concorrentes ). O que ocorre quando elas se intersectam? Isto é, o que ocorre quando = ?
por ViniRFB » Ter Mar 06, 2012 20:58
por fraol » Ter Mar 06, 2012 21:47
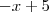crescendo: -3, -2, -1, 0, 1, ... e seja f(x) = mín{
}. (em azul) é menor que o valor de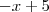 
(em vermelho), então para f(x) interessa o valor de . 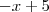(em vermelho) é menor que o valor de (em azul), então para f(x) interessa o valor de .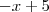
.
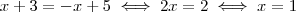
ou
.por fraol » Ter Mar 06, 2012 21:53
por ViniRFB » Qua Mar 07, 2012 17:26
por concurseironf » Qui Ago 21, 2014 12:24
Usuários navegando neste fórum: Nenhum usuário registrado e 20 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a e elevar ao quadrado os dois lados)