Rafael16 escreveu:Resolvi esse sistema abaixo, e minha resposta não coincide com o gabarito. Enfim, não sei onde errei, mas gostaria que me falasse onde.
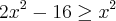
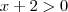
Ok, mas tem uma observação: o termo "raízes" é aplicado para equações. O que você poderia dizer é que x = -4 e x = 4 são as raízes da equação
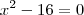
.
Rafael16 escreveu:x + 2 > 0
x + 2 = 0
x = - 2
Está incorreto. Você deveria ter escrito:
x + 2 > 0
x > -2
Rafael16 escreveu:Coloquei na reta real para poder fazer o jogo de sinais, e achei a resposta:
S = {x ? ?|-4 ? x < -2 ou x ? 4}
Errado.
Na primeira inequação, temos que:
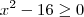
Analisando o sinal da função
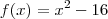
, temos que
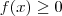
para x em
![(-\infty,\,-4]\cup [4,\,+\infty) (-\infty,\,-4]\cup [4,\,+\infty)](/latexrender/pictures/5726a8224f4e253a968e9b90837d092e.png)
.
Já na segunda inequação, temos que:
x > -2
Ou seja, temos que x está no intervalo
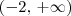
.
Sabemos que a solução do sistema de inequações é a interseção entre a solução de cada uma de suas inequações.
Desse modo, temos que:
![((-\infty,\,-4]\cup [4,\,+\infty)) \cap (-2,\,+\infty) = [4,\,+\infty) ((-\infty,\,-4]\cup [4,\,+\infty)) \cap (-2,\,+\infty) = [4,\,+\infty)](/latexrender/pictures/98da62f1392324febf714c871171f859.png)
.
O gabarito está errado. O correto seria:

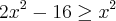
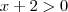
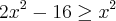
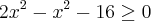
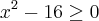
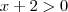
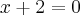



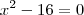 .
.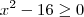
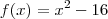 , temos que
, temos que 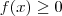 para x em
para x em ![(-\infty,\,-4]\cup [4,\,+\infty) (-\infty,\,-4]\cup [4,\,+\infty)](/latexrender/pictures/5726a8224f4e253a968e9b90837d092e.png) .
.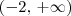 .
.![((-\infty,\,-4]\cup [4,\,+\infty)) \cap (-2,\,+\infty) = [4,\,+\infty) ((-\infty,\,-4]\cup [4,\,+\infty)) \cap (-2,\,+\infty) = [4,\,+\infty)](/latexrender/pictures/98da62f1392324febf714c871171f859.png) .
.


 .
.



