Antes de mais nada, um conjunto sempre vai ter como subconjunto um conjunto vazio
Outra coisa, quando temos, por exemplo, um conjunto A menos um conjunto B, isso quer dizer os elementos que tem no conjunto A mas que NÃO tem no conjunto B. Por exemplo:
A = {1,2,3}
B = {2,3}
A - B = {1}
pois são os elementos que tem em A mas que NÃOtem em B
A - VAZIO = A
isso porque os elementos que tem no conjunto A mas que NÃO tem no Conjunto Vazio é o proprio A
exemplo:
A = {1,2,3}
B = { }
A - B = {1,2,3} ou seja, o próprio A
VAZIO - A = VAZIO
Isso porque não tem nenhum elemento que tem no conjunto vazio que não tem no A, portanto vai ser o próprio VAZIO.
exemplo:
B = { }
A = {1,2,3}
B - A = { } Isso porque não tem nenhum elemento que tem em B mas que NÃO tem em A.
Acho que ficou um pouco redundante

Bom, acho que não provei nada, mas pelo menos acho que deu pra entender um pouco
Abraço!
 um conjunto. Prove que
um conjunto. Prove que 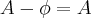 e
e 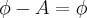 .
.



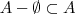 ;
;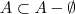 ;
;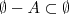 ;
;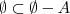 .
. em A. Como o vazio não tem elementos, podemos escrevê-lo como
em A. Como o vazio não tem elementos, podemos escrevê-lo como 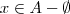 .
. . Então
. Então  mas não está em
mas não está em 

 .
.