 por Cleyson007 » Qua Jun 10, 2009 13:51
por Cleyson007 » Qua Jun 10, 2009 13:51
Olá, boa tarde!
Estou com dúvida na montagem do problema que segue. Penso que o mesmo pode ser resolvido usando o estudo das Progressões. Gostaria de ajuda.
--> Entre cinco pessoas foram repartidas 100 medidas de trigo, de modo que a segunda recebeu a mais do que a primeira o mesmo que a terceira recebeu a mais do que a segunda, que corresponde ao mesmo que a quarta recebeu a mais do que a terceira e também a mesma quantidade que a quinta recebeu a mais do que a quarta. Quanto recebeu cada pessoa?
Agradeço sua ajuda!
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Marcampucio » Qua Jun 10, 2009 14:26
por Marcampucio » Qua Jun 10, 2009 14:26
a primeira recebe

a segunda

a terceira
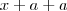
a quarta

a quinta
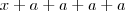
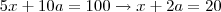
há múltiplas soluções. Vejamos algumas soluções inteiras que ocorrem para os valores
pares de

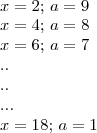
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Cleyson007 » Qua Jun 10, 2009 14:55
por Cleyson007 » Qua Jun 10, 2009 14:55
Marcampucio escreveu:a primeira recebe

a segunda

a terceira
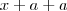
a quarta

a quinta
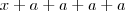
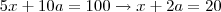
há múltiplas soluções. Vejamos algumas soluções inteiras que ocorrem para os valores
pares de

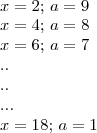
Boa tarde Marcampucio!
Boa explicação

Obrigado pela ajuda.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Quantia Investida
por Cleyson007 » Sex Ago 07, 2009 14:10
- 2 Respostas
- 2068 Exibições
- Última mensagem por Cleyson007

Sex Ago 07, 2009 19:36
Matemática Financeira
-
- Problema quantia do irmão
por junior_gyn » Qua Mai 04, 2011 16:01
- 1 Respostas
- 6720 Exibições
- Última mensagem por Molina

Qua Mai 04, 2011 20:06
Desafios Médios
-
- Pre-Universitario (Trigo...)
 por Pre-Universitario » Qui Ago 11, 2011 17:31
por Pre-Universitario » Qui Ago 11, 2011 17:31
- 2 Respostas
- 3604 Exibições
- Última mensagem por Pre-Universitario

Sex Ago 12, 2011 17:22
Trigonometria
-
- Pre-Universitario (Trigo....)
por Pre-Universitario » Sex Ago 12, 2011 18:07
- 2 Respostas
- 1141 Exibições
- Última mensagem por Pre-Universitario

Dom Ago 14, 2011 20:14
Trigonometria
-
- Pre-Universitario Trigo......
por Pre-Universitario » Qua Ago 24, 2011 18:09
- 0 Respostas
- 730 Exibições
- Última mensagem por Pre-Universitario

Qua Ago 24, 2011 18:09
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





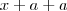

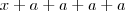
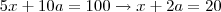
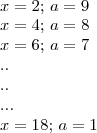

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.