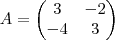 , ache B, de modo que
, ache B, de modo que 
Não sei resolver essa questão, peço a quem souber que me ajude a resolvê-la.
Desde já, agradeço!

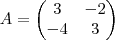 , ache B, de modo que
, ache B, de modo que 

Ana_Rodrigues escreveu:Se, ache B, de modo que
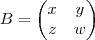
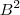 , que é o mesmo que BB, obtemos que:
, que é o mesmo que BB, obtemos que: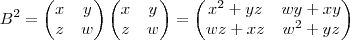
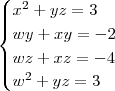

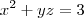
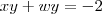
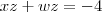
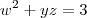



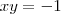



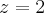
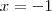
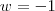

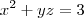
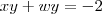
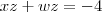
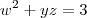



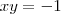



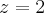
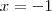
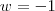

Ana_Rodrigues escreveu:Oi, na verdade meu problema é resolver esse tipo de sistema.
Eu resolvi, talvez esteja incompleto.
(...)
Peço que mostre seu jeito de responder esse sistema!
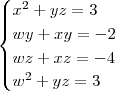
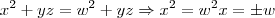
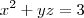
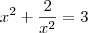
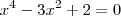
 ,
,  ,
,  e
e  .
.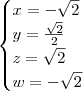
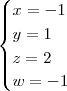
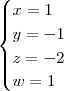
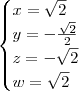

Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



