a- x³-3x²-4x+12 [eu fiz fatoração por agrupamento/fator comum]
x²(x-3)-4(x-3)
=>(x-3)(x²-4) ou (x-3)(x-2)(x+2)
b-
 [eu fiz essa colocando 3x^1/2 em evidencia]
[eu fiz essa colocando 3x^1/2 em evidencia]assim =>
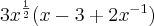
e tem essas simplificação de frações algébricas:

fatorando o 2x²-x-1 usando báskara encontro= (2x-2)(2x+1)
fatorando o x²-9 (diferença de quadrados) encontro = (x-3)(x+3)
assim:
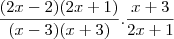
cancelando o (2x+1) da primeira fração com o da segunda, e o x+3
meu resultado ficou igual a
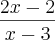
não morram de tédio gente, vamos a ultima
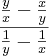
resolvi assim ó:

cancelei o xy da esquerda com o da direita, resultado
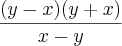
oOo pessoal, se alguém puder conferir se está certo, dizer onde estou errado, se eu deixei alguma incompleta, eu fico muito agradecida.
Obrigada
Deus abençoe
Samara Silva Santos
[/tex]


 [eu fiz essa colocando 3x^1/2 em evidencia]
[eu fiz essa colocando 3x^1/2 em evidencia]
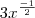 em evidência.
em evidência.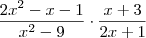
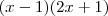 . Use isto agora.
. Use isto agora.

 e vice-versa. Simplifique usando isto.
e vice-versa. Simplifique usando isto.
