 por Rosana Vieira » Dom Fev 19, 2012 10:51
por Rosana Vieira » Dom Fev 19, 2012 10:51
Olá alguém pode me ajudar na resolução deste exercício
Escreva os números reais na forma solicitada em cada item:
a) 36 como potência de base ;
b) como um número inteiro;
c) 729 como potência de expoente 3;
d) 729 como potência de base 3;
e) como um número inteiro.
2. A concentração de um certo medicamento no organismo humano, depois de um tempo t, é dada por , em que C0 é a quantidade inicial ingerida do remédio e P é o tempo de meia-vida da substância no organismo.
Para um determinado anestésico, cujo tempo de meia-vida é de 90 minutos, a concentração mínima que garante seu efeito é de 60 mg por quilograma de peso corporal.
a) Um dentista deve realizar uma pequena cirurgia com duração estimada de 3 horas. Qual deverá ser a dose mínima desse anestésico para um paciente de 60 kg, de modo que ele faça efeito durante toda cirurgia? Justifique.
b)Depois de quanto tempo a anestesia irá perder o efeito em um paciente de 75 kg que tomou uma dose de 36000 mg? Justifique.
3. Segundo o IBGE, os recenseamentos feitos no Brasil nas últimas décadas, a população brasileira nos últimos 70 anos foi a seguinte:
Ano População
1940 41.236.315
1950 51.944.397
1960 70.191.370
1970 93.139.037
1980 119.002.706
1990 146.352.150
2000 169.544.443
2010 190.755.799
a) Sabendo que a taxa de crescimento média r em um período de tempo t é dada por , onde Pf é o tamanho da população no final do período e Pi é o tamanho no início. Calcule a taxa média anual de crescimento nesses últimos 70 anos. Deixe os cálculos como justificativa.
b)Com o valor obtido no item anterior, faça uma estimativa para a população em 2020. Justifique.
Observação: Para esta questão você deverá usar uma calculadora científica.






![\left(\frac{1}{6} \right){}^{-2}=\left(\frac{6}{1} \right){}^{2}=36
b) {27}^{\frac{6}{9}}={27}^{\frac{2}{3}}=\sqrt[3]{{27}^{2}}=\sqrt[3]{729}=9 \left(\frac{1}{6} \right){}^{-2}=\left(\frac{6}{1} \right){}^{2}=36
b) {27}^{\frac{6}{9}}={27}^{\frac{2}{3}}=\sqrt[3]{{27}^{2}}=\sqrt[3]{729}=9](/latexrender/pictures/d7dacbfea8b057e645df05ed13601f86.png)
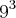
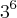
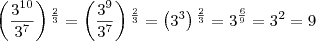







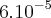 que foi substituído na fórmula no lugar de C(3), não se refere apenas a concentração mínima do remédio por 90min e que no caso, para 3h deveria ser contado o dobro???... Não sei se pensei errado... me dá uma luz....
que foi substituído na fórmula no lugar de C(3), não se refere apenas a concentração mínima do remédio por 90min e que no caso, para 3h deveria ser contado o dobro???... Não sei se pensei errado... me dá uma luz....




 .
.
 :
: