Olá estou com dúvida sobre como fazer essa questão por sistema.
Eu tenho a resolução dela por sistema, mas não entendi como o professor fez para achar a resposta.
A questão é a seguinte:
Certo dia, dois técnicos judiciários - A e B - foram incumbidos de digitar as páginas de um texto e dividiram o total de páginas entre si, em partes inversamentes proporcionais às suas respectivas idades: 24 e 36 anos. Se, ao término dessa tarefa, o número de páginas digitadas por A excedia em 38 unidades, a metade do número de páginas digitadas por B, então o total de páginas do texto era:
Gabarito:
95 páginas
Resolução do prof.
a / 1/2 = b /1/3 ele achou depois 2a=3b. Por quê? Não seria 2b=3a?
O sistema dele ficou assim:
a=b/2 + 38
2a=3b
método por substituição. A partir daí não entendi mais nada.
Conto com ajuda de todos.
Grato
ViniRFB


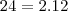 e
e  então ele cancelou os
então ele cancelou os 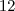 e usou o
e usou o  e
e  para fazer a proporcionalidade inversa, assim:
para fazer a proporcionalidade inversa, assim: e portanto
e portanto  ( lembre-se que dividir por uma fração é o mesmo que multiplicar pelo inverso da fração ).
( lembre-se que dividir por uma fração é o mesmo que multiplicar pelo inverso da fração ).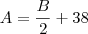 e também usou a expressão encontrada pela proporcionalidade inversa para formar o sisteminha.
e também usou a expressão encontrada pela proporcionalidade inversa para formar o sisteminha. 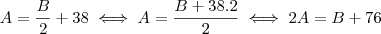 .
. 

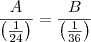 .
.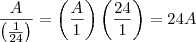 e
e 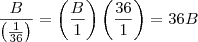 , igualando teremos:
, igualando teremos: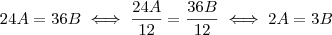 .
.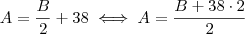
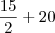 ?
?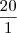 ).
).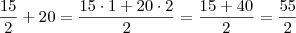
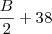 .
.
 .
.
 :
: