 por Claudin » Qui Fev 09, 2012 18:59
por Claudin » Qui Fev 09, 2012 18:59
3. (a) Calcule o determinante da matriz: A =
1 2 2 3
1 0 ?2 0
3 ?1 1 ?2
4 ?3 0 2
(b) O sistema AX = 0 tem solu¸c˜ao n˜ao trivial? ¯ Justi?que.
Como resolver, e o que fazer para resolver?
Não compreendi a questão
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qui Fev 09, 2012 20:13
por MarceloFantini » Qui Fev 09, 2012 20:13
Você sabe calcular o determinante de uma matriz genérica

? Se sim, basta ver se o determinante é nulo ou não. No primeiro caso, isto significaria que

tem soluções não triviais, enquanto que no segundo a única solução é a trivial.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Seg Fev 13, 2012 15:32
por Claudin » Seg Fev 13, 2012 15:32
Gostaria de saber se o
http://www.wolframalpha.com/Cacula também determinante de uma matriz.
Por exemplo nesse exercício eu obtive
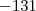
(Corrigi com ajuda do colega Marcelo Fantini)

Queria saber se o resultado realmente é esse?
Editado pela última vez por
Claudin em Seg Fev 13, 2012 16:45, em um total de 2 vezes.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Seg Fev 13, 2012 16:15
por MarceloFantini » Seg Fev 13, 2012 16:15
Procurei aqui e parece que o código para matriz é {{1,2,2,3},{1,0,-2,0},{3,-1,1,-2},{4,-3,0,2}}. Ele retorna a matriz e calcula o determinante também, e a resposta foi -131. Em todo caso, é diferente de zero e portanto a única solução é a trivial.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Seg Fev 13, 2012 16:17
por LuizAquino » Seg Fev 13, 2012 16:17
Claudin escreveu:Gostaria de saber se o
http://www.wolframalpha.com/Cacula também determinante de uma matriz.
Por exemplo nesse exercício eu obtive -89
Queria saber se o resultado realmente é esse?
Sim, é possível calcular determinantes. Veja como acessando a página de exemplos:
Wolfram|Alpha Examples - Matrices & Linear Algebrahttp://www.wolframalpha.com/examples/Matrices.html
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Seg Fev 13, 2012 16:48
por Claudin » Seg Fev 13, 2012 16:48
MarceloFantini escreveu:Procurei aqui e parece que o código para matriz é {{1,2,2,3},{1,0,-2,0},{3,-1,1,-2},{4,-3,0,2}}. Ele retorna a matriz e calcula o determinante também, e a resposta foi -131. Em todo caso, é diferente de zero e portanto a única solução é a trivial.
Não compreendi a explicação da pergunta da letra 'B' ?
Gostaria de saber também se a análise sobre as soluções do sistema linear tem haver com o resultado do determinante, como por exemplo, determinante for maior, menor ou igual a zero, se isso influencia na resposta da letra 'b'?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Seg Fev 13, 2012 16:55
por MarceloFantini » Seg Fev 13, 2012 16:55
O determinante tem relação com a solução de um sistema sim. Se ele for diferente de zero, isso significa que ele possui solução única. No caso de um sistema homogêneo, já sabemos que o vetor nulo é solução, portanto e o determinante for diferente de zero isto nos assegura que esta é realmente a única solução.
Quando o determinante é zero, isto significa que pode existir mais de uma solução ou não existirem soluções. Novamente, como é homogêneio, sabemos que tem solução, e portanto isto significa que existe mais de uma solução.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Seg Fev 13, 2012 17:41
por Claudin » Seg Fev 13, 2012 17:41
Se o determinante for diferente de zero, ele possui solução única.
E se for igual a zero, quais as soluções que ele possui?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Seg Fev 13, 2012 17:47
por MarceloFantini » Seg Fev 13, 2012 17:47
Como eu disse, ele pode ter várias soluções ou nenhuma solução.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Seg Fev 13, 2012 17:59
por Claudin » Seg Fev 13, 2012 17:59
Correto.
Não estava aparecendo aqui o resto de sua explicação.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7170 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
-
- [Matriz]- inversa de uma matriz
por Ana_Rodrigues » Seg Mar 26, 2012 08:54
- 2 Respostas
- 3576 Exibições
- Última mensagem por Ana_Rodrigues

Seg Mar 26, 2012 18:05
Matrizes e Determinantes
-
- [MATRIZ]Determinante da Matriz 4x4
por LAZAROTTI » Qui Mai 03, 2012 22:33
- 1 Respostas
- 6729 Exibições
- Última mensagem por LuizAquino

Sex Mai 11, 2012 08:00
Matrizes e Determinantes
-
- [Matriz] Matriz com potencias
por rochadapesada » Dom Abr 07, 2013 20:29
- 3 Respostas
- 4705 Exibições
- Última mensagem por DanielFerreira

Seg Abr 08, 2013 17:32
Matrizes e Determinantes
-
- matriz
por Barbara » Ter Ago 18, 2009 15:26
- 4 Respostas
- 4814 Exibições
- Última mensagem por Molina

Qui Ago 20, 2009 18:11
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 ? Se sim, basta ver se o determinante é nulo ou não. No primeiro caso, isto significaria que
? Se sim, basta ver se o determinante é nulo ou não. No primeiro caso, isto significaria que  tem soluções não triviais, enquanto que no segundo a única solução é a trivial.
tem soluções não triviais, enquanto que no segundo a única solução é a trivial.

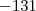 (Corrigi com ajuda do colega Marcelo Fantini)
(Corrigi com ajuda do colega Marcelo Fantini) 










