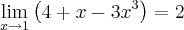
Encontre os valores de
 que correspondam a
que correspondam a 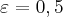 e
e 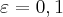
Não consigo resolver essa questão, eu paro em:
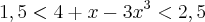 Para
Para 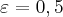
e
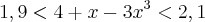 Para
Para 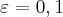

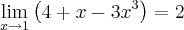
 que correspondam a
que correspondam a 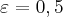 e
e 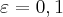
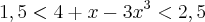 Para
Para 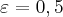
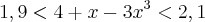 Para
Para 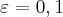

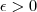 , existe um
, existe um 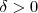 tal que
tal que , então
, então 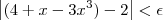 .
.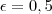 e
e 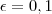 e, também, sabemos que o tal
e, também, sabemos que o tal  é em função de
é em função de  , então para simplificar escolha
, então para simplificar escolha  , ou seja
, ou seja 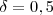 e
e 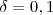 respectivamente.
respectivamente.

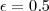 significa dizer que na epsilon-vizinhança de 2, que é o limite, a função varia entre
significa dizer que na epsilon-vizinhança de 2, que é o limite, a função varia entre e
e  . Esta variação no valor da função deve-se ao fato de que x variou na vizinhança de 1 uma quantidade
. Esta variação no valor da função deve-se ao fato de que x variou na vizinhança de 1 uma quantidade  que é função do tal
que é função do tal  .
.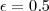 significa que a função variou entre 1,5 e 2,5. Pegando os extremos:
significa que a função variou entre 1,5 e 2,5. Pegando os extremos: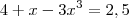 então
então  cuja raiz real é aproximadamente 0,94
cuja raiz real é aproximadamente 0,94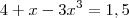 então
então  cuja raiz real é aproximadamente 1,06
cuja raiz real é aproximadamente 1,06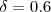 .
.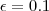 nos levará a
nos levará a  .
.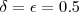 ).
).
 , como eu acho a raiz?
, como eu acho a raiz?
Ana_Rodrigues escreveu:Eu sei como é.
Na verdade minha dúvida é achar a raiz, sem precisar usar uma ferramenta gráfica pra isso.
Em, como eu acho a raiz?


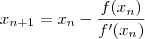
![[0, \,1] [0, \,1]](/latexrender/pictures/4e6005816d25d5de0a8a8af719bb7852.png) , a função troca de sinal, pois
, a função troca de sinal, pois 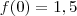 e
e 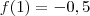 ...
...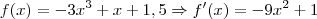 .
. temos um valor mais próximo de zero para f, vamos tomar
temos um valor mais próximo de zero para f, vamos tomar  para inicir a interação. Assim, temos
para inicir a interação. Assim, temos
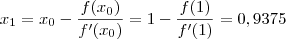
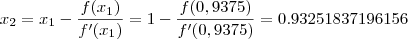
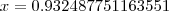

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.