 por nathyn » Qui Jan 26, 2012 17:23
por nathyn » Qui Jan 26, 2012 17:23
Oii, gostaria de uma ajuda com a seguinte questão por favor, é que não sei onde estou errando...
![\sqrt[]{1+x+{x}^{2}} \sqrt[]{1+x+{x}^{2}}](/latexrender/pictures/5458ff43753bc8f70c5c1a9f4f333f9d.png)
![+\sqrt[]{1-x+{x}^{2}} +\sqrt[]{1-x+{x}^{2}}](/latexrender/pictures/a9dd9a67df80168aba8f55330aabbdd9.png)
=4
Elevei ambos os lados ao quadrado e encontrei:

+x+1=16-8
![\sqrt[]{{x}^{2}-x+1}+{x}^{2}-x+1 \sqrt[]{{x}^{2}-x+1}+{x}^{2}-x+1](/latexrender/pictures/63fdc3a90922f70c5e73324f92f753e1.png)

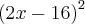
=
![\left({-8\sqrt[]{{x}^{2}-x+1}} \right)^{2} \left({-8\sqrt[]{{x}^{2}-x+1}} \right)^{2}](/latexrender/pictures/572d8dd31234b7bb68e825eb55fac26c.png)

4x-64x+256=64

-64x+64

64

-4x-192=0
Eu fiz assim, porém resolvendo a equação eu nao encontro como resultado um valor igual a resposta do livro que é 4/
![\sqrt[]{5}, -4/\sqrt[]{5} \sqrt[]{5}, -4/\sqrt[]{5}](/latexrender/pictures/e0cf2fc8f2e958292c2bd6f9a4b85424.png)
Se alguem puder me ajudar...
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por nathyn » Qui Jan 26, 2012 19:27
por nathyn » Qui Jan 26, 2012 19:27
Caramba, dei bobeira.
Brigadão =)
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ONDE ESTOU ERRANDO?
por Cleyson007 » Qui Nov 24, 2011 14:09
- 1 Respostas
- 1143 Exibições
- Última mensagem por LuizAquino

Dom Nov 27, 2011 18:57
Matrizes e Determinantes
-
- onde estou errando me ajudem
por weverton » Qua Jun 23, 2010 17:56
- 9 Respostas
- 4484 Exibições
- Última mensagem por weverton

Sáb Jun 26, 2010 03:51
Logaritmos
-
- Expressão , onde estou errando ? ajuda
por LuizCarlos » Qui Ago 04, 2011 23:37
- 8 Respostas
- 3242 Exibições
- Última mensagem por LuizCarlos

Sex Ago 05, 2011 01:40
Álgebra Elementar
-
- Onde estou errando nessa questão?
por LuizCarlos » Dom Nov 27, 2011 14:00
- 3 Respostas
- 1666 Exibições
- Última mensagem por Andreza

Dom Nov 27, 2011 15:19
Álgebra Elementar
-
- Onde estou errando nesse exercício
por LuizCarlos » Dom Abr 08, 2012 13:40
- 5 Respostas
- 2038 Exibições
- Última mensagem por LuizCarlos

Seg Abr 09, 2012 10:55
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{1+x+{x}^{2}} \sqrt[]{1+x+{x}^{2}}](/latexrender/pictures/5458ff43753bc8f70c5c1a9f4f333f9d.png)
![+\sqrt[]{1-x+{x}^{2}} +\sqrt[]{1-x+{x}^{2}}](/latexrender/pictures/a9dd9a67df80168aba8f55330aabbdd9.png) =4
=4 +x+1=16-8
+x+1=16-8![\sqrt[]{{x}^{2}-x+1}+{x}^{2}-x+1 \sqrt[]{{x}^{2}-x+1}+{x}^{2}-x+1](/latexrender/pictures/63fdc3a90922f70c5e73324f92f753e1.png)

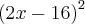 =
=![\left({-8\sqrt[]{{x}^{2}-x+1}} \right)^{2} \left({-8\sqrt[]{{x}^{2}-x+1}} \right)^{2}](/latexrender/pictures/572d8dd31234b7bb68e825eb55fac26c.png)
 4x-64x+256=64
4x-64x+256=64 -64x+64
-64x+64 64
64 -4x-192=0
-4x-192=0![\sqrt[]{5}, -4/\sqrt[]{5} \sqrt[]{5}, -4/\sqrt[]{5}](/latexrender/pictures/e0cf2fc8f2e958292c2bd6f9a4b85424.png)

![\sqrt[]{1+x+{x}^{2}} \sqrt[]{1+x+{x}^{2}}](/latexrender/pictures/5458ff43753bc8f70c5c1a9f4f333f9d.png)
![+\sqrt[]{1-x+{x}^{2}} +\sqrt[]{1-x+{x}^{2}}](/latexrender/pictures/a9dd9a67df80168aba8f55330aabbdd9.png) =4
=4 +x+1=16-8
+x+1=16-8![\sqrt[]{{x}^{2}-x+1}+{x}^{2}-x+1 \sqrt[]{{x}^{2}-x+1}+{x}^{2}-x+1](/latexrender/pictures/63fdc3a90922f70c5e73324f92f753e1.png)

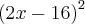 =
=![\left({-8\sqrt[]{{x}^{2}-x+1}} \right)^{2} \left({-8\sqrt[]{{x}^{2}-x+1}} \right)^{2}](/latexrender/pictures/572d8dd31234b7bb68e825eb55fac26c.png)
 4x-64x+256=64
4x-64x+256=64 -64x+64
-64x+64 64
64 -4x-192=0
-4x-192=0![\sqrt[]{5}, -4/\sqrt[]{5} \sqrt[]{5}, -4/\sqrt[]{5}](/latexrender/pictures/e0cf2fc8f2e958292c2bd6f9a4b85424.png)

![{\left(2x-16 \right)}^{2}=\left({-8\sqrt[]{{x}^{2}-x+1}} \right)^{2}\Rightarrow {\left(2x-16 \right)}^{2}=\left({-8\sqrt[]{{x}^{2}-x+1}} \right)^{2}\Rightarrow](/latexrender/pictures/f2a755df3fe8582de15a54f63dfe568d.png)

