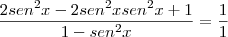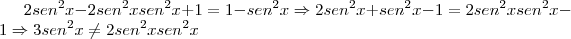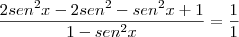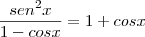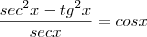por Camila Z » Seg Jan 16, 2012 23:15
por Camila Z » Seg Jan 16, 2012 23:15
Bom, preciso provar que:
(senx+cosx)(senx-cosx)=2sen^2x -1
Estou tentando fazer pela regra do quad. do 1º + 2 vezes os elementos - o quad. do 2º: (senx)^2+2senx.cosx-(cosx)^2, dividi tudo por cosx^2 para obter o 1 do final, mas não consigo chegar na igualdade...
E tb nesta outra igualdade: senx^2/1-cosx + secx^2-tgx^2/secx = 1
Em todas minhas tentativas, sobra o 1 e o cosx tb!
Obrigada
-
Camila Z
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Jan 16, 2012 22:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: formado
 por Arkanus Darondra » Seg Jan 16, 2012 23:56
por Arkanus Darondra » Seg Jan 16, 2012 23:56
A segunda equação é
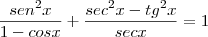
?
Obs: Cuidado! O correto é elevar o sen ao quadrado e não o x.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Camila Z » Ter Jan 17, 2012 14:22
por Camila Z » Ter Jan 17, 2012 14:22
Obrigada, mas eu tenho que detalhar "provando" que dá o quadrado do 1º menos o quadrado do 2º... me ajude

A segunda é isso mesmo... como fica?
-
Camila Z
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Jan 16, 2012 22:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: formado
 por Arkanus Darondra » Ter Jan 17, 2012 20:27
por Arkanus Darondra » Ter Jan 17, 2012 20:27
Camila Z escreveu:Obrigada, mas eu tenho que detalhar "provando" que dá o quadrado do 1º menos o quadrado do 2º... me ajude

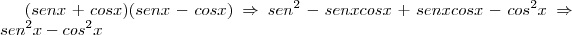
(Diferença de quadrados!)
Camila Z escreveu:A segunda é isso mesmo... como fica?
Não consegui chegar na igualdade. Mas fiz um desenvolvimento. Antes de mostrá-lo, vou esclarecer algumas coisas.
Se
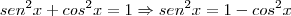
Se
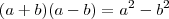
então
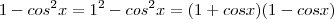
//
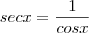
//
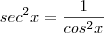
//
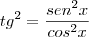
Fiz um desenvolvimento bem detalhado. Se alguém encontrar algo errado, por favor, corrija, pois não consegui resolver a igualdade proposta.
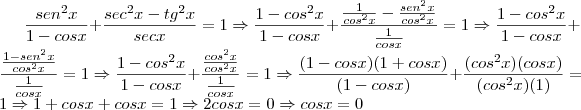
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Ter Jan 17, 2012 21:40
por fraol » Ter Jan 17, 2012 21:40
Arkanus, acompanhei o seu desenvolvimento e o mesmo está correto.
Camila, você já reviu se a segunda expressão é como foi colocada no post?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Camila Z » Ter Jan 17, 2012 22:13
por Camila Z » Ter Jan 17, 2012 22:13
Muito obrigada mesmo, mas vendo o detalhamento da 2ª, eu queria enviar o meu desenvolvimento para vc dar uma olhada... é muito para digitar, como faço para enviar como figura? O meu fica com 1 cosx no final...
Ah, gente, desculpa, recebi uma mensagem de que pode estar errado o sinal de + no meio das frações, parece que é -! Ai sim fica ok, né?
-
Camila Z
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Jan 16, 2012 22:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: formado
 por Arkanus Darondra » Ter Jan 17, 2012 23:19
por Arkanus Darondra » Ter Jan 17, 2012 23:19
Camila Z escreveu:Muito obrigada mesmo, mas vendo o detalhamento da 2ª, eu queria enviar o meu desenvolvimento para vc dar uma olhada... é muito para digitar, como faço para enviar como figura? O meu fica com 1 cosx no final...
Para postar uma imagem basta hospedá-la no site
http://imageshack.us/, pegar o link direto e colocá-lo, na sua mensagem, como em: [img]link[/img]
Camila Z escreveu:Ah, gente, desculpa, recebi uma mensagem de que pode estar errado o sinal de + no meio das frações, parece que é -! Ai sim fica ok, né?
Sim.
Por favor, mande sua resolução para analisarmos.

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Camila Z » Qua Jan 18, 2012 10:03
por Camila Z » Qua Jan 18, 2012 10:03
 http://profile.imageshack.us/user/camilaz/
http://profile.imageshack.us/user/camilaz/Bom... não sei se está certo a postagem da imagem, mas a resolução da identidade tá! rsrs
É o meu 1º desenvolvimento, que tinha feito antes de pedir ajuda pra vcs, está com o sinal + mesmo, não recebi a confirmação de que é - ainda...
-
Camila Z
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Jan 16, 2012 22:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: formado
 por Arkanus Darondra » Qua Jan 18, 2012 11:17
por Arkanus Darondra » Qua Jan 18, 2012 11:17
Camila Z escreveu:
Camila, você fez tudo certo até a terceira linha do seu desenvolvimento.
1º) 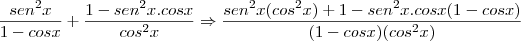
Ou
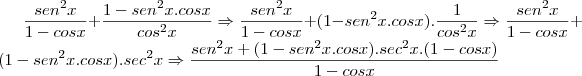
Isto já torna incorreta sua resolução, mas vou destacar outros pontos.
2º) 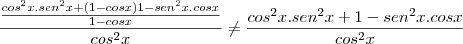
Você não pode cancelar neste caso, pois o
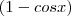
não está em ambos os lados da soma.
3º) 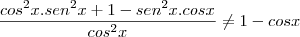
Você cometeu o mesmo erro anterior. Além disso
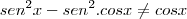
Se eu tiver interpretado errado a sua resolução, ou qualquer dúvida, volte aqui.

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Arkanus Darondra » Qua Jan 18, 2012 23:20
por Arkanus Darondra » Qua Jan 18, 2012 23:20
Camila, não estou conseguindo ver sua resolução. A imagem está meio cortada.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Camila Z » Qui Jan 19, 2012 09:35
por Camila Z » Qui Jan 19, 2012 09:35
Eu cortei a 1ª parte que vc falou que estava certo, mudei só depois da 3ª linha, considerar o início da imagem anterior...
-
Camila Z
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Jan 16, 2012 22:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: formado
 por Arkanus Darondra » Qui Jan 19, 2012 11:19
por Arkanus Darondra » Qui Jan 19, 2012 11:19
Camila, a parte que eu disse ser correta são as 3 primeiras linhas da sua resolução anterior. Nesta imagem aparece apenas da última linha em diante.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Camila Z » Qui Jan 19, 2012 14:29
por Camila Z » Qui Jan 19, 2012 14:29
-
Camila Z
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Jan 16, 2012 22:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: formado
 por Arkanus Darondra » Qui Jan 19, 2012 15:37
por Arkanus Darondra » Qui Jan 19, 2012 15:37
Antepenúltima linha) 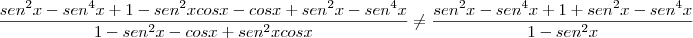
Para você cancelar o
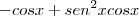
do denominador, é necessário você colocá-lo em evidência tanto no numerador quanto no denominador.
Última linha) Também não concordo com:
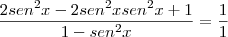
Para isso ser verdade, então:
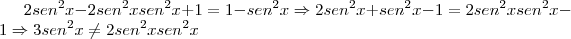
Seria verdade se:
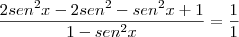
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Arkanus Darondra » Qui Jan 19, 2012 15:41
por Arkanus Darondra » Qui Jan 19, 2012 15:41
Para resolver este exercício, seria mais fácil se você notasse que:
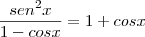
e que
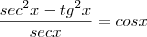
Então
 Obs:
Obs: Olhe a resolução que fiz acima.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Camila Z » Qui Jan 19, 2012 19:25
por Camila Z » Qui Jan 19, 2012 19:25
Ok, obrigada.
-
Camila Z
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Jan 16, 2012 22:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




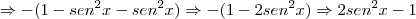

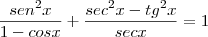 ?
?



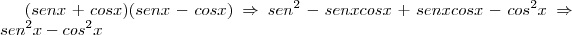 (Diferença de quadrados!)
(Diferença de quadrados!)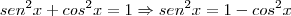
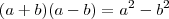 então
então 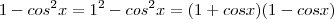 //
//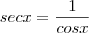 //
//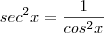 //
//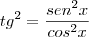
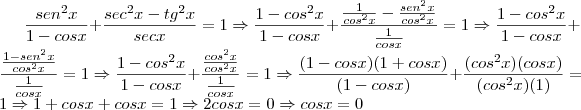






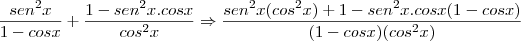
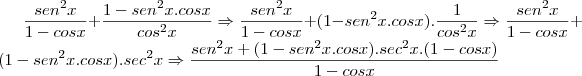
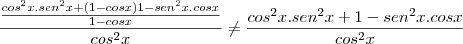
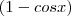 não está em ambos os lados da soma.
não está em ambos os lados da soma.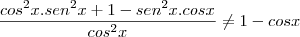
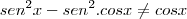








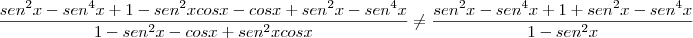
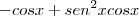 do denominador, é necessário você colocá-lo em evidência tanto no numerador quanto no denominador.
do denominador, é necessário você colocá-lo em evidência tanto no numerador quanto no denominador.