Gostaria que alguém me ajudasse com uma função, na verdade não quero a solução do problema, só quero entender como "lidar" com a questão abaixo.
![[\frac{2x^2}{x^2+1}] = x [\frac{2x^2}{x^2+1}] = x](/latexrender/pictures/be586c672c5b5ab35fde1eb5df6f4362.png)
Onde
![[x] [x]](/latexrender/pictures/3e5314e9fd31509fdeb83faa0f729ba2.png) é o menor inteiro maior ou igual a x.
é o menor inteiro maior ou igual a x.E aí está a minha dúvida, posso lidar com essa equação como uma equação "normal" ou tem algum detalhe que não sei ??? Mais uma vez muito obrigado, não precisa resolver o problema só quero "o caminho das pedras"...
[ ]'s
Renato.
EDITADO:
Na verdade o nome dessa função é função teto, então a equação seria:
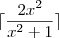
Acho que consigo fazer algum progresso agora..
EDITADO 2:
Esqueçam, já resolvi !!!


 , qual seria o resultado? Como confirmá-lo? Como fazer isso algebricamente?
, qual seria o resultado? Como confirmá-lo? Como fazer isso algebricamente?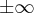 ) ou quando se aproxima de zero, ou seja, utilizando limite e somente depois fazer a intersecção com a função desejada. Isso porque é difícil saber o comportamento da função que você postou.
) ou quando se aproxima de zero, ou seja, utilizando limite e somente depois fazer a intersecção com a função desejada. Isso porque é difícil saber o comportamento da função que você postou.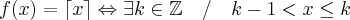 , teremos
, teremos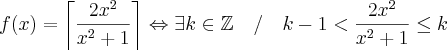
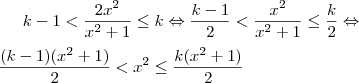 .
.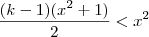 , temos
, temos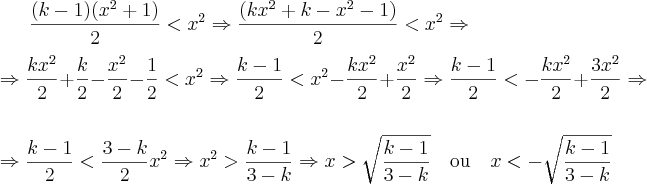 .
. , teremos
, teremos 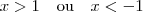 .
.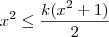 , teremos
, teremos .
. , então
, então  .
. , então
, então 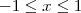 .
.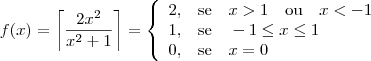
 com a função
com a função 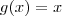 .
. e
e  .
.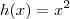 , os pontos seriam
, os pontos seriam 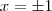 .
.