 por thiagocsouza » Ter Jan 03, 2012 22:41
por thiagocsouza » Ter Jan 03, 2012 22:41
Observando a idade de 3 amigas, um matemático verificou que a idade de Ana somada ao dobro da idade de Brenda é igual a 69, a diferença entre as idades de Cássia e de Brenda é de 6 anos. e que a soma das idades das 3 amigas dá 75. Cássia tem:
a) 31
b) 29
c) 27
d) 25
Porque a Resposta é 25 ?
-
thiagocsouza
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jan 03, 2012 22:37
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Neperiano » Qua Jan 04, 2012 22:39
por Neperiano » Qua Jan 04, 2012 22:39
Ola
Ana = x
Brenda = y
Cássia = Z
x + 2y = 69
z - y = 6
x + y + z = 75
Só resolver o sistema e descobrir z
Qualquer duvida
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Arkanus Darondra » Qua Jan 04, 2012 23:43
por Arkanus Darondra » Qua Jan 04, 2012 23:43
thiagocsouza escreveu:Observando a idade de 3 amigas, um matemático verificou que a idade de Ana somada ao dobro da idade de Brenda é igual a 69, a diferença entre as idades de Cássia e de Brenda é de 6 anos. e que a soma das idades das 3 amigas dá 75. Cássia tem:
a) 31
b) 29
c) 27
d) 25
Considerando o sistema
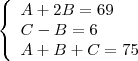
Onde Ana = A, Brenda = B e Cássia = C
Temos um sistema onde todos os valores de C das alternativa são possíveis, desde correspondam às equações:
B = C - 6
A = 81 - 2C
É possível chegar a estas equações por meio do escalonamento do sistema:
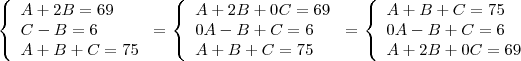
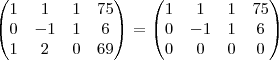
Como a última linha é nula, temos um SPI
Adotando

, chegamos às equações.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por thiagocsouza » Qui Jan 05, 2012 09:26
por thiagocsouza » Qui Jan 05, 2012 09:26
Não me ajudaram em nada, essa questão caiu no vestibular do SENAI. Já afirmei que a resposta é 25, segundo o gabarito divulgado. Agora não consegui achar esse resultado.
-
thiagocsouza
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jan 03, 2012 22:37
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Neperiano » Qui Jan 05, 2012 14:23
por Neperiano » Qui Jan 05, 2012 14:23
Ola
Nem precisar resolver por escalonamento, se você isolar x na primeira e z na segunda, é só substituir na 3, irá descobrir y, e a partir dai vai desobrindo as outras.
E tiagocsouza o objetivo do forum não é resolver a questão para você, é dar os caminhos para você chegar até lá, tente você mesmo fazer por um dos jeitos supracitados, mostre seu passo a passo que corrijiremos se algo estiver errado.
Tente fazer
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Arkanus Darondra » Qui Jan 05, 2012 15:37
por Arkanus Darondra » Qui Jan 05, 2012 15:37
Dessa forma, provavelmente, falta algum dado da questão
Visto que, ao substituir-se
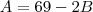

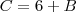
na última equação, não encontraremos o valor de

.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Neperiano » Qui Jan 05, 2012 15:42
por Neperiano » Qui Jan 05, 2012 15:42
Ola
Arkanus Darondra escreveu:thiagocsouza escreveu:Observando a idade de 3 amigas, um matemático verificou que a idade de Ana somada ao dobro da idade de Brenda é igual a 69, a diferença entre as idades de Cássia e de Brenda é de 6 anos. e que a soma das idades das 3 amigas dá 75. Cássia tem:
a) 31
b) 29
c) 27
d) 25
Considerando o sistema
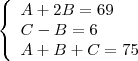
Onde Ana = A, Brenda = B e Cássia = C
Temos um sistema onde todos os valores de C das alternativa são possíveis, desde correspondam às equações:
B = C - 6
A = 81 - 2C
É possível chegar a estas equações por meio do escalonamento do sistema:
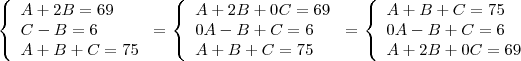
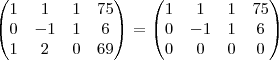
Como a última linha é nula, temos um SPI
Adotando

, chegamos às equações.
A = 69 - 2B
C = 6 + B
Logo
69 - 2B + B + 6 + B = 75
Tem razão os b se anulam, só dar para resolver por escalonamento mesmo, você está correto
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por DanielFerreira » Sáb Jan 07, 2012 21:55
por DanielFerreira » Sáb Jan 07, 2012 21:55
thiagocsouza escreveu:Observando a idade de 3 amigas, um matemático verificou que a idade de Ana somada ao dobro da idade de Brenda é igual a 69, a diferença entre as idades de Cássia e de Brenda é de 6 anos. e que a soma das idades das 3 amigas dá 75. Cássia tem:
a) 31
b) 29
c) 27
d) 25
Porque a Resposta é 25 ?
A + 2B = 69
C - B = 6
A + B + C = 75
---------------------
2A + 2B + 2C = 150
A + B + C = 75
Temos 3 variáveis e 2 equações, pode-se concluir que o sistema, assim como já foi dito, é INDETERMINADO. Ou seja, Thiago, possui mais que uma solução!
Nesse caso, terá que resolver pelas alternativas!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Arkanus Darondra » Sáb Jan 07, 2012 22:12
por Arkanus Darondra » Sáb Jan 07, 2012 22:12
Falta algum dado na questão, visto que qualquer valor da alternativa satisfaz o sistema.
Para C = 31, temos que B = 25 e A = 19
Para C = 29, temos que B = 23 e A = 23
Para C = 27, temos que B = 21 e A = 27
Para C = 25, temos que B = 19 e A = 31
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema Matemático
por honorio » Dom Set 06, 2009 20:06
- 10 Respostas
- 7708 Exibições
- Última mensagem por honorio

Dom Set 20, 2009 17:25
Funções
-
- Problema matematico
por girotto » Seg Jun 11, 2012 16:34
- 1 Respostas
- 1696 Exibições
- Última mensagem por Russman

Seg Jun 11, 2012 18:50
Sistemas de Equações
-
- problema matemático de vendas
por vb_evan » Sáb Mar 06, 2010 15:20
- 2 Respostas
- 3040 Exibições
- Última mensagem por vb_evan

Dom Mar 07, 2010 09:16
Dúvidas Pendentes (aguardando novos colaboradores)
-
- duvida em um problema matematico
por diogo_poa » Ter Mar 23, 2010 23:15
- 0 Respostas
- 1363 Exibições
- Última mensagem por diogo_poa

Ter Mar 23, 2010 23:15
Sistemas de Equações
-
- Porcentagem - Problema matemático
por Sheyla » Qua Mar 27, 2013 14:21
- 3 Respostas
- 3469 Exibições
- Última mensagem por Sheyla

Qua Mar 27, 2013 21:42
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



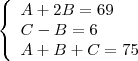
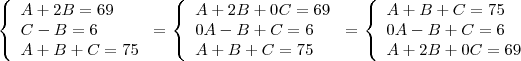
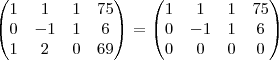
 , chegamos às equações.
, chegamos às equações.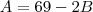

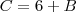 na última equação, não encontraremos o valor de
na última equação, não encontraremos o valor de  .
.