Oi!
O assunto é bem simples mas eu fiz e ficou diferente do gabarito.
Lá vai:
QUANTO VALE SENO240-COS570+SEN330-COS2460?
Minha resolução:
Sen240 =raiz de 3 /2
cos570= raiz de 3/2
sen330 = sen 150 (não sei resolver)
cos2460 = -1
Essa eu também não consegui:
Determine o valor da expressãp tg(11pi) + tg(9pi/4) - tg25pi/6
Eu fiz :
Tg11pi = tg180 = 0
tg9pi/4 = tg45 = 1
tg25pi/6 = tg30 = raiz de 3/2
Então, são duas questões fáceis mas não consegui resolve-las.
Ficaria grato quem puder me ajudar.


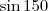 . Na segunda questão basta substituir e calcular, qual foi a dificuldade?
. Na segunda questão basta substituir e calcular, qual foi a dificuldade?

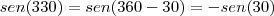
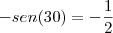 .
.
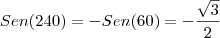
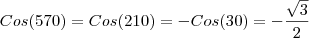
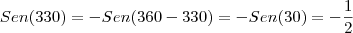
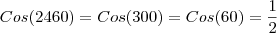
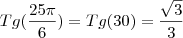
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)