 por Andreza » Ter Jan 03, 2012 10:43
por Andreza » Ter Jan 03, 2012 10:43
Sobre um quadrado ABCD, de lado de 4cm, determinamos os pontos M,N,P e Q de tal forma que AM=BN=CP=DQ=x. Qual é a área de MNPQ, em centímetros quadrados e em função de x?
Calculando a área separadamente do quadrando cincunscrito tenho 16cm².
Aplicando teorema de pitágoras tenho L= 4+x
Como faço pra encontrar a coesão das ideias e juntar para montar a resposta?
Dede já agradeço.
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por Andreza » Ter Jan 03, 2012 11:18
por Andreza » Ter Jan 03, 2012 11:18
Estou tentando resolver ele aqui e encontrei
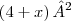
= x² + 8x+16.
Porém nao é esta a resposta correta q está no gabarito da FCC.
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por fraol » Ter Jan 03, 2012 13:54
por fraol » Ter Jan 03, 2012 13:54
Oi Andreza,
Veja se este desenvolvimento confere:
Chamando de
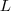
o lado do paralelogramo formado conforme o enunciado então a área de MNPQ será
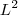
.
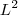
sai por Pitágoras ao analisarmos o triângulo, por exemplo, AMQ que terá hipotenusa
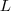
e catetos

e

, então:
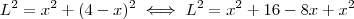
e, portanto:
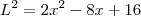
.
Ok?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Área do Quadrado
por Pri Ferreira » Qua Mar 21, 2012 14:35
- 3 Respostas
- 2314 Exibições
- Última mensagem por ednaldo1982

Sáb Mar 31, 2012 11:48
Geometria Plana
-
- Porcentagem, area do quadrado
por lucas7 » Ter Mar 01, 2011 09:51
- 3 Respostas
- 7845 Exibições
- Última mensagem por lucas7

Ter Mar 01, 2011 13:47
Problemas do Cotidiano
-
- Quadrado - Área, corda, porcentagem.
por Alexander » Sáb Abr 23, 2011 12:08
- 3 Respostas
- 7769 Exibições
- Última mensagem por Alexander

Dom Abr 24, 2011 11:15
Geometria Plana
-
- Mostre que a área do quadrado é menor que a do hexagono
por andersontricordiano » Qua Abr 06, 2011 16:30
- 1 Respostas
- 2028 Exibições
- Última mensagem por Elcioschin

Qua Abr 06, 2011 18:04
Geometria Plana
-
- Calcular perímetro do quadrado] através da área do triângulo
 por lukasmetal » Qua Nov 30, 2011 12:11
por lukasmetal » Qua Nov 30, 2011 12:11
- 3 Respostas
- 3860 Exibições
- Última mensagem por lukasmetal

Qui Dez 01, 2011 12:19
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


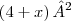 = x² + 8x+16.
= x² + 8x+16.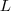 o lado do paralelogramo formado conforme o enunciado então a área de MNPQ será
o lado do paralelogramo formado conforme o enunciado então a área de MNPQ será 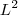 .
.  e
e  , então:
, então: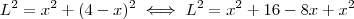 e, portanto:
e, portanto: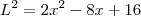 .
.