(a) O volume V da caixa em função de x;
(b) A área S da caixa em função de x.
Por favor poderia me dizer algumas dicas de como poderia resolver esta questão?
Estou sem
 !
!Por favor me ajude!


 !
!

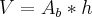 , onde
, onde 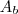 é a área da base e
é a área da base e  é a altura.
é a altura.



Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: