Tenho andado a estudar e surgiu esta dúvida. Como não estava a encontrar solução satisfatória em lado nenhum para o meu problema, pensei que vocês me pudessem ajudar.
O enunciado é o seguinte:
Mostrar, a partir da definição, que
A minha resolução começou por ser esta, no entanto estou bloqueado a meio do processo e não sei como passar daí.
![\forall\:\delta>0\:\exists\varepsilon>0:0<\left|\right|(x,y)\:-\:(0,0)\left| \right|<\varepsilon\Rightarrow\left|(x^2+y^2)sin\left(\frac{1}{\sqrt[]{x^2+y^2}} \right)\right|<\delta \forall\:\delta>0\:\exists\varepsilon>0:0<\left|\right|(x,y)\:-\:(0,0)\left| \right|<\varepsilon\Rightarrow\left|(x^2+y^2)sin\left(\frac{1}{\sqrt[]{x^2+y^2}} \right)\right|<\delta](/latexrender/pictures/2afa654872713064a2a31991b8f2ec59.png)
![\forall\:\delta>0\:\exists\varepsilon>0:0<\sqrt[]{x^2+y^2}<\varepsilon\Rightarrow\left|(x^2+y^2)sin\left(\frac{1}{\sqrt[]{x^2+y^2}} \right)\right|<\delta \forall\:\delta>0\:\exists\varepsilon>0:0<\sqrt[]{x^2+y^2}<\varepsilon\Rightarrow\left|(x^2+y^2)sin\left(\frac{1}{\sqrt[]{x^2+y^2}} \right)\right|<\delta](/latexrender/pictures/5f83ea4b61088cb03347026478260890.png)
Aqui fiquei bloqueado porque não sei como resolver tendo um seno na função.
![\left|(x^2+y^2)sin\left(\frac{1}{\sqrt[]{x^2+y^2}} \right) \right|=(x^2+y^2)\left|sin\left(\frac{1}{\sqrt[]{x^2+y^2}} \right) \right| \left|(x^2+y^2)sin\left(\frac{1}{\sqrt[]{x^2+y^2}} \right) \right|=(x^2+y^2)\left|sin\left(\frac{1}{\sqrt[]{x^2+y^2}} \right) \right|](/latexrender/pictures/8e00b5a0fa42181e64f03309c3b82cba.png)

![\lim_{(x,y)\rightarrow(0,0)} (x^2+y^2) sin\left(\frac{1}{\sqrt[]{x^2+y^2}}\right) = 0 \lim_{(x,y)\rightarrow(0,0)} (x^2+y^2) sin\left(\frac{1}{\sqrt[]{x^2+y^2}}\right) = 0](/latexrender/pictures/3adcb2962442f6460c5203568ab07048.png)

 tende a zero no limite, logo a função total vai tender a zero quando o par x,y tender a zero...
tende a zero no limite, logo a função total vai tender a zero quando o par x,y tender a zero... 
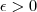 , existe
, existe 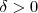 tal que se
tal que se 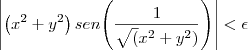 então
então 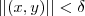 .
.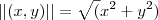 . Então vamos lá:
. Então vamos lá: ( a preencher).
( a preencher).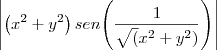
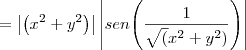
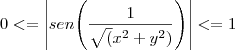 , então devemos ter
, então devemos ter 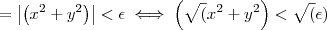 .
.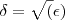 e concluímos que:
e concluímos que: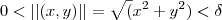 ou seja:
ou seja: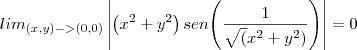 .
.
 .
.
 :
: