 por sullivan » Ter Dez 27, 2011 12:14
por sullivan » Ter Dez 27, 2011 12:14
Galera confesso que o problema é simples, mas vou falar a verdade eu não consegui nem montar o sistema dele por favor alguem me da uma direção para eu fazer ele..
A soma dos valores absolutos de um número de dois algarismos é 13. Trocando-se a ordem desses algarismos, obtém-se um número que tem 27 unidades a mais que o primeiro. Qual é esse número?
-
sullivan
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sex Dez 23, 2011 10:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Ter Dez 27, 2011 13:54
por fraol » Ter Dez 27, 2011 13:54
Olá Sullivan,
Tenho uma sugestão:
Sejam

e

os algarismos, assim os dois números são
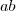
e
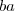
e
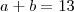
e
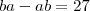
.
Obs:
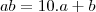
e
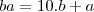
.
Acho que dá pra resolver assim, o que você acha?
Abç,
Francisco.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por sullivan » Ter Dez 27, 2011 14:05
por sullivan » Ter Dez 27, 2011 14:05
por que o número 10 multiplicando a e b?
-
sullivan
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sex Dez 23, 2011 10:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Ter Dez 27, 2011 14:33
por fraol » Ter Dez 27, 2011 14:33
Oi,
Por exemplo o número 38:
38 = 3 . 10 + 8.
Ok?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por sullivan » Ter Dez 27, 2011 14:44
por sullivan » Ter Dez 27, 2011 14:44
ok vou tentar fazer só um minuto.. =)
-
sullivan
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sex Dez 23, 2011 10:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por sullivan » Ter Dez 27, 2011 15:00
por sullivan » Ter Dez 27, 2011 15:00
criei o seguinte sistema
a+b=13
ba - ab=27
substituindo :: 10.b+a - 10.a+b=27
onde b = 13-a
então ficou
10.(13-a) + a - 10.a + 13 -a = 27
calculando.. a = 58
porem b=-45
não entendi como achar o b já que deu negativo deve ter algo errado =/
-
sullivan
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sex Dez 23, 2011 10:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Ter Dez 27, 2011 15:15
por fraol » Ter Dez 27, 2011 15:15
10b + a - ( 10a + b ) = 27 ( cuidado com o sinal aqui )
10b + a - 10a - b = 27
9b + b + a - 9a - a - b = 27
9b + 13 - 9a - (a + b) = 27
9(b - a) = 27
b - a = 3
13 - a - a = 3
-2a = -10
a = 5 e b = 8.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por sullivan » Ter Dez 27, 2011 15:26
por sullivan » Ter Dez 27, 2011 15:26
entendi muito obrigado pela dica
acho que hoje nao estou legal rs com sua primeira dica eu deveria ter achado a resposta sozinho, na próxima eu consigo =)
-
sullivan
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sex Dez 23, 2011 10:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Ter Dez 27, 2011 15:28
por fraol » Ter Dez 27, 2011 15:28
Valeu,
Eu tb vivo errando nos sinais e nas continhas, faz parte ...
Abç.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema Simples
por SamiraDias » Qua Dez 28, 2011 21:22
- 1 Respostas
- 1046 Exibições
- Última mensagem por MarceloFantini

Qui Dez 29, 2011 12:36
Álgebra Elementar
-
- Problema de juro simples!
por LuizCarlos » Qui Set 15, 2011 17:09
- 1 Respostas
- 1199 Exibições
- Última mensagem por MarceloFantini

Qua Set 21, 2011 22:13
Álgebra Elementar
-
- Porcentagem - Problema Simples
por rio51964 » Dom Out 13, 2013 23:36
- 0 Respostas
- 1923 Exibições
- Última mensagem por rio51964

Dom Out 13, 2013 23:36
Álgebra Elementar
-
- Problema juros simples, dúvida.
por elisamaria » Seg Mar 09, 2015 16:15
- 0 Respostas
- 3953 Exibições
- Última mensagem por elisamaria

Seg Mar 09, 2015 16:15
Matemática Financeira
-
- Problema envolvendo desconto comercial simples
por Ju_Petrokis » Qua Set 16, 2009 20:00
- 1 Respostas
- 2584 Exibições
- Última mensagem por Victor Emanuel

Qui Set 24, 2009 15:30
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 e
e  os algarismos, assim os dois números são
os algarismos, assim os dois números são 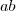 e
e 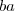 e
e 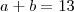 e
e 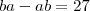 .
.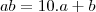 e
e 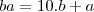 .
.