FAP0153
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por andersontricordiano » Qui Dez 15, 2011 11:44
por andersontricordiano » Qui Dez 15, 2011 11:44
A figura seguir representa um bloco de massa igual a
![0,2\sqrt[]{2} 0,2\sqrt[]{2}](/latexrender/pictures/54d2a940473cbb927d1cb25ee3afe564.png)
kg, apoiado um plano inclinado. O ângulo

, entre o plano inclinado e o plano horizontal é igual a 45º . sabe-se que o coeficiente de atrito estático entre o bloco e o plano inclinado é igual a 0,5 e que a aceleração da gravidade local é 10,0 m/s². Qual deverá ser o menor valor da força F (em N) para que o bloco fique em repouso sobre o plano inclinado?
Resposta:
![0,55\sqrt[]{2} 0,55\sqrt[]{2}](/latexrender/pictures/1e8136418bfbc49f7c555474b270e0b2.png)
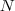
Agradeço quem resolver esse calculo!!
Você não está autorizado a ver ou baixar esse anexo.
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Fabricio dalla » Sáb Dez 17, 2011 22:14
por Fabricio dalla » Sáb Dez 17, 2011 22:14
R=Px-(Fat+F)
para parar
R=0
Px=Fat+F
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por andersontricordiano » Ter Dez 20, 2011 16:28
por andersontricordiano » Ter Dez 20, 2011 16:28
eu fiz desse jeito, porem não cheguei a resposta
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Ter Dez 20, 2011 20:32
por MarceloFantini » Ter Dez 20, 2011 20:32
Mostre todas as suas contas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por andersontricordiano » Ter Dez 20, 2011 21:55
por andersontricordiano » Ter Dez 20, 2011 21:55
px= p * sen45º=
![0,2\sqrt[]{2}*10*\frac{\sqrt[]{2}}{2}=2 0,2\sqrt[]{2}*10*\frac{\sqrt[]{2}}{2}=2](/latexrender/pictures/bf546a11c90fb4244d077bb5ff8572f8.png)

==
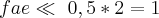
Px=Fat + F ===> 2=1+F ==> F=1N
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Fabricio dalla » Sex Dez 23, 2011 15:57
por Fabricio dalla » Sex Dez 23, 2011 15:57
é sei não então
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Mecânica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Qual é o menor e o maior valor de x na expressão
por andersontricordiano » Seg Out 03, 2011 16:56
- 1 Respostas
- 3945 Exibições
- Última mensagem por MarceloFantini

Seg Out 03, 2011 21:10
Trigonometria
-
- Força resultante sobre a esfera menor
por Cleyson007 » Dom Mai 12, 2013 16:45
- 2 Respostas
- 2964 Exibições
- Última mensagem por Cleyson007

Dom Mai 12, 2013 21:56
Física
-
- Qual é o menor número natural que....
por antonioCoisas » Qua Jan 12, 2011 15:32
- 0 Respostas
- 2621 Exibições
- Última mensagem por antonioCoisas

Qua Jan 12, 2011 15:32
Álgebra Elementar
-
- menor valor de x
por stuart clark » Sáb Mai 28, 2011 00:41
- 0 Respostas
- 1800 Exibições
- Última mensagem por stuart clark

Sáb Mai 28, 2011 00:41
Trigonometria
-
- Função do 2° grau - o menor valor numa expressão
por PeterHiggs » Sex Mai 25, 2012 22:24
- 1 Respostas
- 2347 Exibições
- Última mensagem por PeterHiggs

Sáb Mai 26, 2012 16:09
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![0,2\sqrt[]{2} 0,2\sqrt[]{2}](/latexrender/pictures/54d2a940473cbb927d1cb25ee3afe564.png) kg, apoiado um plano inclinado. O ângulo
kg, apoiado um plano inclinado. O ângulo  , entre o plano inclinado e o plano horizontal é igual a 45º . sabe-se que o coeficiente de atrito estático entre o bloco e o plano inclinado é igual a 0,5 e que a aceleração da gravidade local é 10,0 m/s². Qual deverá ser o menor valor da força F (em N) para que o bloco fique em repouso sobre o plano inclinado?
, entre o plano inclinado e o plano horizontal é igual a 45º . sabe-se que o coeficiente de atrito estático entre o bloco e o plano inclinado é igual a 0,5 e que a aceleração da gravidade local é 10,0 m/s². Qual deverá ser o menor valor da força F (em N) para que o bloco fique em repouso sobre o plano inclinado?![0,55\sqrt[]{2} 0,55\sqrt[]{2}](/latexrender/pictures/1e8136418bfbc49f7c555474b270e0b2.png)
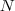




![0,2\sqrt[]{2}*10*\frac{\sqrt[]{2}}{2}=2 0,2\sqrt[]{2}*10*\frac{\sqrt[]{2}}{2}=2](/latexrender/pictures/bf546a11c90fb4244d077bb5ff8572f8.png)
 ==
==