Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por joaofonseca » Seg Dez 12, 2011 22:59
por joaofonseca » Seg Dez 12, 2011 22:59
Alguém consegue decifrar qual a expressão analitica deste gráfico?
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por joaofonseca » Ter Dez 13, 2011 17:07
por joaofonseca » Ter Dez 13, 2011 17:07
Este problema mostra que quem dominar as transformações de funções conseguirá resolver muitos problemas sobre funções de forma simples.
Pela observação do gráfico, pode-se identificar o gráfico parcial de duas parabolas.O gráfico parcial da parabola da direita é identico ao gráfico parcial da parabola da esquerda.Conclui-se que qualquer que tenha sido a transformação a que a função tenha sido sujeita, a função trasformada trata os valores negativos de
x da mesma forma que os valores positivos de
x.Qual é a operação matemática que devolve valores positivos independentemente dos valores introduzidos?
É o valor absoluto!Neste caso, como temos uma reflexão em relação ao eixo Oy, temos g(x)=f(|x|).Agora basta analizar a parte direita do gráfico e escrever a expressão analitica para a parabola.
Na expressão

, c=-2. Sabemos também que um dos zeros é o 2.Encontrar o outro zero é que se torna dificil.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qui Dez 15, 2011 17:48
por LuizAquino » Qui Dez 15, 2011 17:48
joaofonseca escreveu:Alguém consegue decifrar qual a expressão analitica deste gráfico?
joaofonseca escreveu:Este problema mostra que quem dominar as transformações de funções conseguirá resolver muitos problemas sobre funções de forma simples.
Pela observação do gráfico, pode-se identificar o gráfico parcial de duas parabolas.O gráfico parcial da parabola da direita é identico ao gráfico parcial da parabola da esquerda.Conclui-se que qualquer que tenha sido a transformação a que a função tenha sido sujeita, a função trasformada trata os valores negativos de x da mesma forma que os valores positivos de x.Qual é a operação matemática que devolve valores positivos independentemente dos valores introduzidos?
É o valor absoluto!Neste caso, como temos uma reflexão em relação ao eixo Oy, temos g(x)=f(|x|).Agora basta analizar a parte direita do gráfico e escrever a expressão analitica para a parabola.
Na expressão

, c=-2. Sabemos também que um dos zeros é o 2.Encontrar o outro zero é que se torna dificil.
Note que há infinitas parábolas tais que y(0) = -2 e y(2) = 0. Portanto, é necessário fazer mais alguma suposição para encontrar apenas uma expressão analítica.
Faça a suposição de que o vértice da parábola tem abscissa igual a 1/2. Isso é razoável com o gráfico. Vide a figura abaixo.
Desse modo, sabemos que
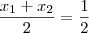
. Lembrando que
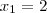
, temos que

.
Além disso, sabemos que outra forma de escrever a parábola é dada por
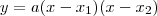
, ou seja, podemos dizer que
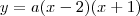
. Agora lembrando que y(0) = -2, determinamos que a = 1. Isso significa que
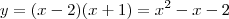
.
Substituindo x por |x|, ficamos com
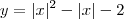
, o que é o mesmo que

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Determinaçao de Zeros de uma expressao analitica]
por R0nny » Sáb Mai 04, 2013 21:53
- 0 Respostas
- 1862 Exibições
- Última mensagem por R0nny

Sáb Mai 04, 2013 21:53
Funções
-
- Expressão
por geriane » Qui Abr 22, 2010 12:49
- 4 Respostas
- 3894 Exibições
- Última mensagem por geriane

Sáb Abr 24, 2010 10:50
Trigonometria
-
- Expressão em PG
por Carolziiinhaaah » Qua Jun 16, 2010 21:10
- 1 Respostas
- 2009 Exibições
- Última mensagem por MarceloFantini

Qua Jun 16, 2010 21:39
Progressões
-
- EXPRESSAO
 por JOHNY » Dom Set 05, 2010 15:26
por JOHNY » Dom Set 05, 2010 15:26
- 1 Respostas
- 2094 Exibições
- Última mensagem por MarceloFantini

Seg Set 06, 2010 13:14
Álgebra Elementar
-
- expressão
por jose henrique » Qua Fev 16, 2011 18:16
- 11 Respostas
- 7749 Exibições
- Última mensagem por jose henrique

Seg Fev 28, 2011 19:39
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 , c=-2. Sabemos também que um dos zeros é o 2.Encontrar o outro zero é que se torna dificil.
, c=-2. Sabemos também que um dos zeros é o 2.Encontrar o outro zero é que se torna dificil.
, c=-2. Sabemos também que um dos zeros é o 2.Encontrar o outro zero é que se torna dificil.
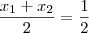 . Lembrando que
. Lembrando que 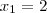 , temos que
, temos que  .
.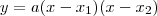 , ou seja, podemos dizer que
, ou seja, podemos dizer que 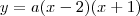 . Agora lembrando que y(0) = -2, determinamos que a = 1. Isso significa que
. Agora lembrando que y(0) = -2, determinamos que a = 1. Isso significa que 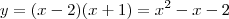 .
.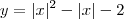 , o que é o mesmo que
, o que é o mesmo que  .
.

 .
.



