Alguém consegue decifrar qual a expressão analitica deste gráfico?



 , c=-2. Sabemos também que um dos zeros é o 2.Encontrar o outro zero é que se torna dificil.
, c=-2. Sabemos também que um dos zeros é o 2.Encontrar o outro zero é que se torna dificil.
joaofonseca escreveu:Alguém consegue decifrar qual a expressão analitica deste gráfico?
joaofonseca escreveu:Este problema mostra que quem dominar as transformações de funções conseguirá resolver muitos problemas sobre funções de forma simples.
Pela observação do gráfico, pode-se identificar o gráfico parcial de duas parabolas.O gráfico parcial da parabola da direita é identico ao gráfico parcial da parabola da esquerda.Conclui-se que qualquer que tenha sido a transformação a que a função tenha sido sujeita, a função trasformada trata os valores negativos de x da mesma forma que os valores positivos de x.Qual é a operação matemática que devolve valores positivos independentemente dos valores introduzidos?
É o valor absoluto!Neste caso, como temos uma reflexão em relação ao eixo Oy, temos g(x)=f(|x|).Agora basta analizar a parte direita do gráfico e escrever a expressão analitica para a parabola.
Na expressão, c=-2. Sabemos também que um dos zeros é o 2.Encontrar o outro zero é que se torna dificil.
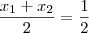 . Lembrando que
. Lembrando que 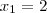 , temos que
, temos que  .
.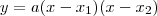 , ou seja, podemos dizer que
, ou seja, podemos dizer que 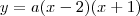 . Agora lembrando que y(0) = -2, determinamos que a = 1. Isso significa que
. Agora lembrando que y(0) = -2, determinamos que a = 1. Isso significa que 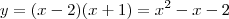 .
.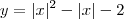 , o que é o mesmo que
, o que é o mesmo que  .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)