Olá,
Você pode resolver esse problema seguindo os passos abaixo:
(1) Faça uma mudança de bases conveniente, isto é, escreva

(2) Agora inverta

e
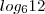
na última igualdade acima, perfeitamente possível, por quê?
(3) Sabendo que
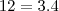
, aplique a propriedade logarítmica que transforma logaritmo de produto em soma de logaritmos.
(4) Bom, se tudo correu bem até aqui você deve levar
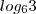
para o primeiro membro da igualdade que desenvolveu em (3).
(5) Assim você vai ficar com uma nova igualdade com
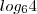
no segundo membro.
(6) Agora é que vem um pequeno artifício matemático: multiplique ambos os membros dessa nova igualdade por 2.
(7) Finalmente, (des)aplique a propriedade logarítmica do expoente no segundo membro que você obterá
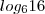
.
(8) Assim você resolve a questão apresentando a resposta em função de

.
Espero que você consiga resolver assim, caso tenha alguma dúvida manda de volta aqui pro forum.
Até mais,
Francisco.
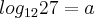 , então
, então 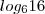 será igual a quanto?
será igual a quanto?


 e
e 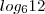 na última igualdade acima, perfeitamente possível, por quê?
na última igualdade acima, perfeitamente possível, por quê?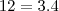 , aplique a propriedade logarítmica que transforma logaritmo de produto em soma de logaritmos.
, aplique a propriedade logarítmica que transforma logaritmo de produto em soma de logaritmos.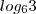 para o primeiro membro da igualdade que desenvolveu em (3).
para o primeiro membro da igualdade que desenvolveu em (3).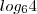 no segundo membro.
no segundo membro. 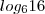 .
. .
. 

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)