 por liviabgomes » Qui Dez 01, 2011 14:59
por liviabgomes » Qui Dez 01, 2011 14:59

- anexo com a conta
podem me ajudar? tenho que fazer pela transformada de laplace??
brigada pela atenção.
-
liviabgomes
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Mai 30, 2011 16:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática licenciatura
- Andamento: cursando
 por LuizAquino » Dom Dez 04, 2011 12:08
por LuizAquino » Dom Dez 04, 2011 12:08
liviabgomes escreveu:Resolva o seguinte problema de valor inicial
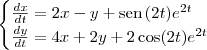
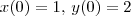
podem me ajudar? tenho que fazer pela transformada de laplace??
Você pode fazer pela Transformada de Laplace. Para isso, siga os passos abaixo.
Passo 1Aplique a Transformada de Laplace em cada equação.
![\begin{cases}
{\cal L}\left[\frac{dx}{dt}\right] = {\cal L}\left[2x - y + \textrm{sen}\,(2t)e^{2t}\right] \\
{\cal L}\left[\frac{dy}{dt}\right] = {\cal L}\left[4x + 2y + 2\cos(2t)e^{2t}\right] \\
\end{cases} \begin{cases}
{\cal L}\left[\frac{dx}{dt}\right] = {\cal L}\left[2x - y + \textrm{sen}\,(2t)e^{2t}\right] \\
{\cal L}\left[\frac{dy}{dt}\right] = {\cal L}\left[4x + 2y + 2\cos(2t)e^{2t}\right] \\
\end{cases}](/latexrender/pictures/37cae2d71e475668ee60fff69a818cfa.png)
![\begin{cases}
s{\cal L}\left[x\right] - x(0) = 2{\cal L}\left[ x\right] - {\cal L}\left[y \right] + {\cal L}\left[\textrm{sen}\,(2t)e^{2t} \right]\\
s{\cal L}\left[y\right] - y(0) = 4{\cal L}\left[ x\right] + 2{\cal L}\left[y \right] + 2{\cal L}\left[\cos(2t)e^{2t} \right] \\
\end{cases} \begin{cases}
s{\cal L}\left[x\right] - x(0) = 2{\cal L}\left[ x\right] - {\cal L}\left[y \right] + {\cal L}\left[\textrm{sen}\,(2t)e^{2t} \right]\\
s{\cal L}\left[y\right] - y(0) = 4{\cal L}\left[ x\right] + 2{\cal L}\left[y \right] + 2{\cal L}\left[\cos(2t)e^{2t} \right] \\
\end{cases}](/latexrender/pictures/097cb65d6cdf2f05a528bb576e42d59e.png)
![\begin{cases}
(s-2){\cal L}\left[x\right] + {\cal L}\left[y \right] = 1 + \frac{2}{(s-2)^2 + 4}\\
-4{\cal L}\left[x\right] + (s-2){\cal L}\left[y\right] = 2 + \frac{2(s-2)}{(s-2)^2 + 4} \\
\end{cases} \begin{cases}
(s-2){\cal L}\left[x\right] + {\cal L}\left[y \right] = 1 + \frac{2}{(s-2)^2 + 4}\\
-4{\cal L}\left[x\right] + (s-2){\cal L}\left[y\right] = 2 + \frac{2(s-2)}{(s-2)^2 + 4} \\
\end{cases}](/latexrender/pictures/a2e3acd5754211a4556bbb326dd8cdc3.png) Passo 2
Passo 2Resolva o sistema anterior para
![{\cal L}\left[x \right] {\cal L}\left[x \right]](/latexrender/pictures/c5dbcff8ffc04e553b59b9b812a0f831.png)
e
![{\cal L}\left[y \right] {\cal L}\left[y \right]](/latexrender/pictures/19f8e2275ea6c09a354531644c8ba5f9.png)
.
![{\cal L}\left[x\right] = -\frac{2}{(s-2)^2 + 4} + \frac{s-2}{(s-2)^2 + 4} {\cal L}\left[x\right] = -\frac{2}{(s-2)^2 + 4} + \frac{s-2}{(s-2)^2 + 4}](/latexrender/pictures/853073365d8682833b65f2a04313c089.png)
![{\cal L}\left[y\right] = \frac{4}{(s-2)^2 + 4} + \frac{8}{\left[(s-2)^2 + 4\right]^2} + \frac{2(s-2)}{(s-2)^2 + 4} + \frac{2(s-2)^2}{\left[(s-2)^2 + 4\right]^2} {\cal L}\left[y\right] = \frac{4}{(s-2)^2 + 4} + \frac{8}{\left[(s-2)^2 + 4\right]^2} + \frac{2(s-2)}{(s-2)^2 + 4} + \frac{2(s-2)^2}{\left[(s-2)^2 + 4\right]^2}](/latexrender/pictures/7a4ab23a6c815a7ad2504976d0b084a5.png) Passo 3
Passo 3Aplique a Transformada Inversa de Laplace na solução do sistema.
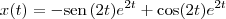
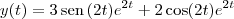 Passo 4
Passo 4Substitua as funções

e

no problema original para conferir a resposta.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por liviabgomes » Dom Dez 04, 2011 20:55
por liviabgomes » Dom Dez 04, 2011 20:55
muito obrigada pela ajuda, foi muito válido.. eu tinha trancado na transformada, e não tinha feito ela inversa depois.. me clareou as ideias.. hahaha. Lá no final para substituir no problema original como eu faço? pego a resposta e boto no lugar de x(t) e y(t) e derivo para ver se da certo?
-
liviabgomes
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Mai 30, 2011 16:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática licenciatura
- Andamento: cursando
 por LuizAquino » Seg Dez 05, 2011 10:15
por LuizAquino » Seg Dez 05, 2011 10:15
liviabgomes escreveu:Lá no final para substituir no problema original como eu faço? pego a resposta e boto no lugar de x(t) e y(t) e derivo para ver se da certo?
Sim.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por liviabgomes » Seg Dez 05, 2011 11:36
por liviabgomes » Seg Dez 05, 2011 11:36
deeeu, brigada!
-
liviabgomes
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Mai 30, 2011 16:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática licenciatura
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Calculo de logaritmo) Resolva em R a seguinte equação
por andersontricordiano » Qua Ago 03, 2011 13:39
- 1 Respostas
- 1713 Exibições
- Última mensagem por Guill

Qua Ago 03, 2011 15:17
Logaritmos
-
- [Equação diferencial] Problema de valor inicial
por Aliocha Karamazov » Qua Fev 15, 2012 23:34
- 2 Respostas
- 1804 Exibições
- Última mensagem por Aliocha Karamazov

Qui Fev 23, 2012 23:43
Cálculo: Limites, Derivadas e Integrais
-
- Equações diferenciais - problema de valor inicial
por emsbp » Qui Abr 12, 2012 18:14
- 0 Respostas
- 1030 Exibições
- Última mensagem por emsbp

Qui Abr 12, 2012 18:14
Cálculo: Limites, Derivadas e Integrais
-
- Resolva, em R, a seguinte inequação
por andersontricordiano » Sex Out 28, 2011 16:06
- 4 Respostas
- 2831 Exibições
- Última mensagem por TheoFerraz

Sex Out 28, 2011 16:55
Logaritmos
-
- Resolva em R a seguinte inequação:
por andersontricordiano » Sex Out 28, 2011 19:47
- 1 Respostas
- 1528 Exibições
- Última mensagem por Aliocha Karamazov

Sex Out 28, 2011 23:11
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![\begin{cases}
{\cal L}\left[\frac{dx}{dt}\right] = {\cal L}\left[2x - y + \textrm{sen}\,(2t)e^{2t}\right] \\
{\cal L}\left[\frac{dy}{dt}\right] = {\cal L}\left[4x + 2y + 2\cos(2t)e^{2t}\right] \\
\end{cases} \begin{cases}
{\cal L}\left[\frac{dx}{dt}\right] = {\cal L}\left[2x - y + \textrm{sen}\,(2t)e^{2t}\right] \\
{\cal L}\left[\frac{dy}{dt}\right] = {\cal L}\left[4x + 2y + 2\cos(2t)e^{2t}\right] \\
\end{cases}](/latexrender/pictures/37cae2d71e475668ee60fff69a818cfa.png)
![\begin{cases}
s{\cal L}\left[x\right] - x(0) = 2{\cal L}\left[ x\right] - {\cal L}\left[y \right] + {\cal L}\left[\textrm{sen}\,(2t)e^{2t} \right]\\
s{\cal L}\left[y\right] - y(0) = 4{\cal L}\left[ x\right] + 2{\cal L}\left[y \right] + 2{\cal L}\left[\cos(2t)e^{2t} \right] \\
\end{cases} \begin{cases}
s{\cal L}\left[x\right] - x(0) = 2{\cal L}\left[ x\right] - {\cal L}\left[y \right] + {\cal L}\left[\textrm{sen}\,(2t)e^{2t} \right]\\
s{\cal L}\left[y\right] - y(0) = 4{\cal L}\left[ x\right] + 2{\cal L}\left[y \right] + 2{\cal L}\left[\cos(2t)e^{2t} \right] \\
\end{cases}](/latexrender/pictures/097cb65d6cdf2f05a528bb576e42d59e.png)
![\begin{cases}
(s-2){\cal L}\left[x\right] + {\cal L}\left[y \right] = 1 + \frac{2}{(s-2)^2 + 4}\\
-4{\cal L}\left[x\right] + (s-2){\cal L}\left[y\right] = 2 + \frac{2(s-2)}{(s-2)^2 + 4} \\
\end{cases} \begin{cases}
(s-2){\cal L}\left[x\right] + {\cal L}\left[y \right] = 1 + \frac{2}{(s-2)^2 + 4}\\
-4{\cal L}\left[x\right] + (s-2){\cal L}\left[y\right] = 2 + \frac{2(s-2)}{(s-2)^2 + 4} \\
\end{cases}](/latexrender/pictures/a2e3acd5754211a4556bbb326dd8cdc3.png)
![{\cal L}\left[x \right] {\cal L}\left[x \right]](/latexrender/pictures/c5dbcff8ffc04e553b59b9b812a0f831.png) e
e ![{\cal L}\left[y \right] {\cal L}\left[y \right]](/latexrender/pictures/19f8e2275ea6c09a354531644c8ba5f9.png) .
.![{\cal L}\left[x\right] = -\frac{2}{(s-2)^2 + 4} + \frac{s-2}{(s-2)^2 + 4} {\cal L}\left[x\right] = -\frac{2}{(s-2)^2 + 4} + \frac{s-2}{(s-2)^2 + 4}](/latexrender/pictures/853073365d8682833b65f2a04313c089.png)
![{\cal L}\left[y\right] = \frac{4}{(s-2)^2 + 4} + \frac{8}{\left[(s-2)^2 + 4\right]^2} + \frac{2(s-2)}{(s-2)^2 + 4} + \frac{2(s-2)^2}{\left[(s-2)^2 + 4\right]^2} {\cal L}\left[y\right] = \frac{4}{(s-2)^2 + 4} + \frac{8}{\left[(s-2)^2 + 4\right]^2} + \frac{2(s-2)}{(s-2)^2 + 4} + \frac{2(s-2)^2}{\left[(s-2)^2 + 4\right]^2}](/latexrender/pictures/7a4ab23a6c815a7ad2504976d0b084a5.png)
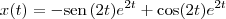
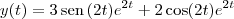
 e
e  no problema original para conferir a resposta.
no problema original para conferir a resposta.


