 por joaofonseca » Sáb Dez 03, 2011 19:40
por joaofonseca » Sáb Dez 03, 2011 19:40
Esta é uma questão de um exame nacional de Matematica em Portugal.
Eu consegui encontrar a resposta graficamente:
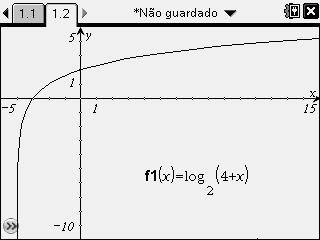
- questao.jpg (10.67 KiB) Exibido 2156 vezes
Como se pode ver quando
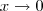
,
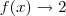
.
Mas não consegui resolver analiticamente.Não consegui resolver a parte:
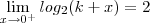
Como é posivel resolver a equação logaritmica dentro do limite?
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por joaofonseca » Sáb Dez 03, 2011 21:07
por joaofonseca » Sáb Dez 03, 2011 21:07
Então podemos afirmar que:
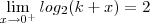
e
![log_{2} \left[ \lim_{x \to 0^+}(k+x) \right]=2 log_{2} \left[ \lim_{x \to 0^+}(k+x) \right]=2](/latexrender/pictures/cbc50454fee1189f4a7adbd9aa1f5774.png)
são a mesma coisa?!?
Na segunda expressão, primeiro calcula-se o limite e depois resolve-se a equação logaritmica.
Obrigado
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Sáb Dez 03, 2011 21:27
por LuizAquino » Sáb Dez 03, 2011 21:27
joaofonseca escreveu:Então podemos afirmar que:
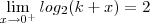
e
![log_{2} \left[ \lim_{x \to 0^+}(k+x) \right]=2 log_{2} \left[ \lim_{x \to 0^+}(k+x) \right]=2](/latexrender/pictures/cbc50454fee1189f4a7adbd9aa1f5774.png)
são a mesma coisa?!?
De modo geral, é verdadeira a seguinte afirmação:
Se
f é contínua em
L e
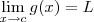
, então
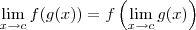
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
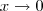 ,
,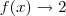 .
.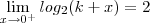


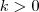 , você pode resolver o limite diretamente:
, você pode resolver o limite diretamente: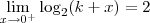

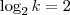
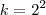


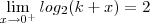
![log_{2} \left[ \lim_{x \to 0^+}(k+x) \right]=2 log_{2} \left[ \lim_{x \to 0^+}(k+x) \right]=2](/latexrender/pictures/cbc50454fee1189f4a7adbd9aa1f5774.png)
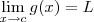 , então
, então 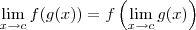 .
. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.